VSEPR Theory Explained with Easy Diagrams

Molecules are not static blobs of atoms randomly stuck together. Instead, they are dynamic three-dimensional structures, each with a precise shape. This shape determines how molecules interact, how they taste or smell, how they react chemically, and how they fit together in the elaborate machinery of life.

But how do chemists predict the shape of a molecule?

Enter the Valence Shell Electron Pair Repulsion (VSEPR) Theory—a simple, elegant, and surprisingly accurate model that allows us to visualize and predict molecular geometry just by looking at the atoms and their valence electrons.

In this article, we will unravel the beauty of VSEPR theory using intuitive explanations, memorable analogies, and hand-drawn-style diagrams to make even the most complex geometries feel approachable. By the end, you’ll not only understand how VSEPR works—you’ll be able to predict the shape of most molecules with confidence.

What Is VSEPR Theory?

The Valence Shell Electron Pair Repulsion (VSEPR) theory is based on one central idea:

Electron pairs around a central atom repel each other and arrange themselves as far apart as possible in 3D space to minimize repulsion.

Imagine trying to sit evenly spaced around a dinner table with strangers. You’ll all spread out to keep personal space. Electrons do the same.

Developed in the 1950s by Ronald Gillespie and Ronald Nyholm, VSEPR theory became a cornerstone of molecular geometry. Though it doesn’t account for bond lengths or orbital hybridization, it’s incredibly useful for predicting shapes, bond angles, and electron pair distribution.

Step-by-Step: How to Use VSEPR

To determine the shape of a molecule using VSEPR, follow these steps:

1. Draw the Lewis structure of the molecule.
2. Count the number of electron pairs (bonding and non-bonding) around the central atom.
3. Determine the electron domain geometry based on repulsion.
4. Account for lone pairs to find the actual molecular shape.
5. Estimate bond angles based on geometry.

Let’s apply this to real examples shortly. But first, let’s dig deeper into what electron pairs are and why lone pairs matter.

Bonding vs. Lone Pairs

An electron domain is any place where electrons are likely to be found around the central atom. These domains can be:

• Bonding pairs: shared between atoms to form covalent bonds.
• Lone pairs (non-bonding pairs): unshared electrons on the central atom.

Lone pairs occupy more space than bonding pairs. Why? Because they are attracted only to one nucleus (the central atom), they spread out more and push bonding pairs closer together, distorting ideal angles.

So the number of electron domains determines the electron geometry, but lone pairs affect the molecular geometry.

Let’s walk through each possible geometry.

Linear Geometry (2 Electron Domains)

Electron Geometry: Linear
Molecular Shape: Linear
Bond Angle: 180°

Example: Carbon Dioxide (CO₂)

Lewis Structure:

O=C=O

• Central atom: C
• 2 double bonds (2 bonding domains)
• No lone pairs

Electron pairs: 2 → Arrange in a straight line to minimize repulsion.

Shape: Linear

Diagram:
(Center: C, double bonded to each O at 180° angle)

→ O ═ C ═ O ←

Other examples:

• Beryllium chloride (BeCl₂)
• Hydrogen cyanide (HCN)

Trigonal Planar (3 Electron Domains)

Electron Geometry: Trigonal Planar
Bond Angle: 120°

Example 1: Boron Trifluoride (BF₃)

Lewis Structure:

F—B—F
     |
     F

• Central atom: B
• 3 single bonds, no lone pairs

Shape: Trigonal Planar (flat triangle)

Diagram:

 F
 |

F — B — F

All fluorines lie in the same plane, 120° apart.

Example 2: Formaldehyde (CH₂O)

• 2 single bonds and 1 double bond
• Still counts as 3 regions of electron density
• Also trigonal planar

Bent (3 Electron Domains, 1 Lone Pair)

Molecular Geometry: Bent
Electron Geometry: Trigonal Planar
Bond Angle: ~117° (less than 120° due to lone pair repulsion)

Example: Sulfur Dioxide (SO₂)

Lewis Structure:

O—S—O
 (.. lone pair)

• 1 lone pair, 2 bonding pairs

Diagram:

 O
/

S

O

The lone pair squashes the angle slightly.

Tetrahedral Geometry (4 Electron Domains)

Electron Geometry: Tetrahedral
Bond Angle: 109.5°

Example: Methane (CH₄)

• Central atom: C
• 4 single bonds
• No lone pairs

Shape: Tetrahedral

Diagram (simplified 3D):

     H
     |
 H—C—H
     |
     H

In 3D space, these hydrogens point to the corners of a tetrahedron.

Trigonal Pyramidal (4 Domains, 1 Lone Pair)

Molecular Geometry: Trigonal Pyramidal
Electron Geometry: Tetrahedral
Bond Angle: ~107°

Example: Ammonia (NH₃)

• Central atom: N
• 3 single bonds
• 1 lone pair

Diagram:

 H
 |

H — N — H
..
The lone pair pushes the bonds downward into a pyramid.

Bent (4 Domains, 2 Lone Pairs)

Molecular Geometry: Bent
Electron Geometry: Tetrahedral
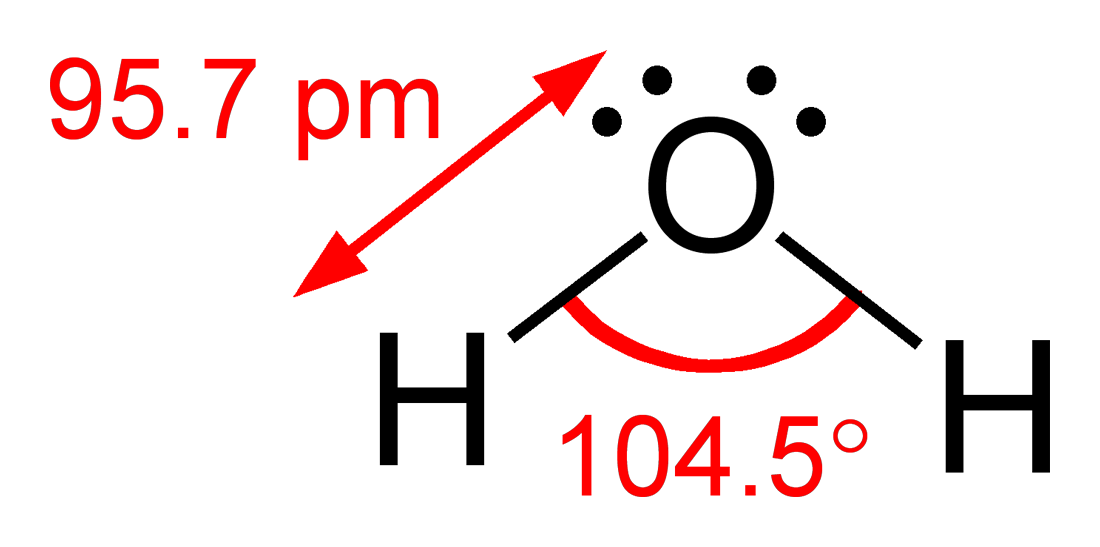
Bond Angle: ~104.5°

Example: Water (H₂O)

Diagram:

H—O—H
 ..
 ..

The two lone pairs compress the bond angle more than in ammonia.

Trigonal Bipyramidal (5 Domains)

Electron Geometry: Trigonal Bipyramidal
Bond Angles: 90° and 120°

Example: Phosphorus Pentachloride (PCl₅)

• Central atom: P
• 5 single bonds

Diagram:

Three atoms in a horizontal plane, two above and below:

 Cl
  |

Cl — P — Cl
|
Cl

• Equatorial positions: 120°
• Axial positions: 90°

Seesaw (5 Domains, 1 Lone Pair)

Example: Sulfur Tetrafluoride (SF₄)

• 4 bonding pairs, 1 lone pair (placed in equatorial position)

Shape: Seesaw

Diagram:

F
|
F—S—F
|
F
..
(Lone pair occupies one of the equatorial spots)

T-Shaped (5 Domains, 2 Lone Pairs)

Example: Chlorine Trifluoride (ClF₃)

• 3 bonding pairs
• 2 lone pairs

Diagram:

F
|

F—Cl—F
..
..

Linear (5 Domains, 3 Lone Pairs)

Example: Xenon Difluoride (XeF₂)

• 2 bonding pairs, 3 lone pairs

Diagram:

F — Xe — F
.. .. ..

All three lone pairs are on equatorial positions, leaving linear bonds.

Octahedral (6 Domains)

Electron Geometry: Octahedral
Bond Angles: 90°

Example: Sulfur Hexafluoride (SF₆)

• 6 bonding pairs, no lone pairs

Shape: Octahedral

Diagram:

F

F — S — F
/
F

Two above, two below, and two in the plane.

Square Pyramidal (6 Domains, 1 Lone Pair)

Example: Bromine Pentafluoride (BrF₅)

• 5 bonding pairs, 1 lone pair

Shape: Square pyramidal (like a 4-legged table with a roof)

Square Planar (6 Domains, 2 Lone Pairs)

Example: Xenon Tetrafluoride (XeF₄)

• 4 bonding pairs, 2 lone pairs

Shape: Square planar (flat)

Diagram:

F—Xe—F
| |
F F
.. ..

Hybridization vs. VSEPR

VSEPR tells us shape. But sometimes you’ll hear terms like sp, sp², sp³. That’s hybridization—how atomic orbitals blend.

Luckily, hybridization usually aligns with VSEPR:

• 2 domains → sp (linear)
• 3 domains → sp² (trigonal planar)
• 4 domains → sp³ (tetrahedral)
• 5 domains → sp³d (trigonal bipyramidal)
• 6 domains → sp³d² (octahedral)

Think of hybridization as the “engine” under the hood, while VSEPR shows the visible car body.

Limitations of VSEPR

While VSEPR is powerful, it isn’t perfect. It doesn’t:

• Account for multiple bonds’ effects on shape
• Explain why lone pairs repel more
• Predict exact bond angles when resonance is involved
• Handle metallic bonding or delocalized systems well

More advanced models (like MO theory and computational chemistry) go further—but for most simple molecules, VSEPR does the job.

Why It Matters: Real-World Applications

Molecular shape affects:

• Reactivity: Will molecules collide correctly to react?
• Taste & smell: Different shapes, different receptor activation
• Drug design: Shape-based “lock and key” interactions
• Materials: Shape dictates crystal packing and conductivity
• Climate: CO₂’s linear shape allows IR absorption—vital to greenhouse effect

From pharmaceuticals to perfumes, from proteins to plastics—shape rules.

Conclusion: The Geometry of Life

VSEPR theory is more than a classroom tool—it’s a way to understand the geometry of matter itself.

Every chemical you encounter, every breath you take, every scent you smell—is governed in part by the shapes of molecules, which are determined by tiny, invisible repulsions between electrons.

This theory gives you a mental microscope—an ability to peer into the hidden dimensions of the world around you and see that even in chaos, there is elegant, mathematical beauty.

In the end, VSEPR is not just about repulsion—it’s about space, balance, and the quiet order that shapes our chemical reality.