For nearly a century, physicists have had a solid grasp of the fundamental laws governing elementary particles. Quantum mechanics, born in the early 20th century, explains the strange and often counterintuitive world of electrons, photons, and quarks. But understanding the rules is only the first step. The real challenge arises when many particles interact with one another, giving rise to behaviors that are not apparent from the properties of individual particles alone.
This is the essence of the quantum many-body problem, a central puzzle in physics. Unlike simple systems with a handful of particles, many-body systems can involve countless interacting quantum states, producing collective phenomena that defy straightforward analysis. Superconductivity, magnetism, exotic topological phases of matter—all emerge from this collective quantum dance.
As Nobel laureate Philip W. Anderson once said, “More is different.” Even though the underlying rules may be known, the emergent behavior is so rich and complex that it requires new ways of thinking. Solving these problems is not just about curiosity—it’s about unlocking the physics behind future technologies, from quantum computers to advanced materials.
Why Conventional Approaches Fall Short
When facing systems with many degrees of freedom, physicists have long relied on approximations. Perturbation theory, for instance, allows researchers to treat interactions as small corrections to otherwise simple systems. But here lies the problem: in strongly interacting quantum systems, the very assumption of “weak interactions” collapses. The phenomena of interest—high-temperature superconductivity or strongly correlated quantum materials—simply cannot be captured by these methods.
On top of that, brute-force computation is not an option. The complexity of quantum many-body systems grows exponentially with the number of particles involved. Simulating just a few dozen interacting particles with full quantum detail would require computational resources larger than any computer on Earth. New strategies are essential, and this is where insights from quantum information theory have begun to change the game.
The Promise of Tensor Networks
A breakthrough came from recognizing a key feature of many-body systems: low-energy quantum states often exhibit relatively low levels of entanglement compared to arbitrary quantum states. This means that while the full quantum wavefunction of a system may be unimaginably large, only a small corner of the quantum landscape is physically relevant.
This realization gave rise to tensor network methods. Instead of trying to store the impossible—every detail of the full quantum state—tensor networks cleverly compress information, capturing the entanglement structure in efficient ways. Among these methods, matrix product states (MPS) and matrix product operators (MPO) stand out as powerful tools, especially in one-dimensional quantum systems.
Tensor networks are not just mathematical tricks; they represent a deep physical truth. By encoding the way particles are entangled, they allow researchers to simulate the emergent properties of matter that were once inaccessible to direct computation.
A New Strategy for the Many-Body Frontier
Recently, a collaboration between researchers at the University of Cambridge, the Institut des Hautes Études Scientifiques, and Ghent University introduced a significant advance in tensor network-based simulation. Their approach, published in Nature Physics, extends the capabilities of existing methods by uniting abstract mathematical frameworks with practical computational tools.
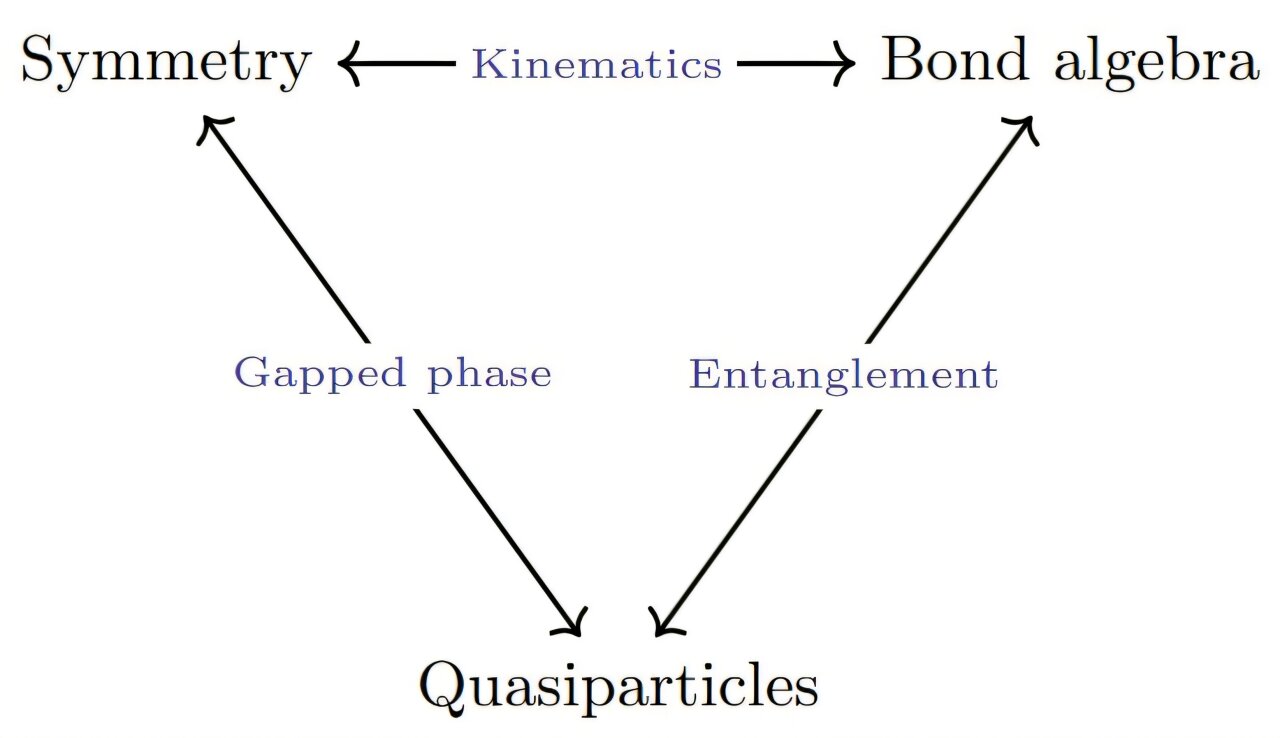
At the heart of their strategy is the use of generalized symmetries, encoded in mathematical structures known as fusion categories. These symmetries go beyond ordinary group theory, providing a richer language for describing how quantum particles can organize themselves. The researchers showed that matrix product operators naturally encode these symmetries, giving a new way to represent the hidden rules shaping many-body quantum states.
By doing so, they could map any one-dimensional quantum Hamiltonian with symmetry onto a dual Hamiltonian with the same energy spectrum but a ground state that spontaneously breaks the symmetry. This breakthrough means that instead of struggling with redundancies enforced by symmetric approaches, the new method reveals a simplified—but still exact—representation of the system.
Breaking Symmetry to Find Order
Symmetry is often celebrated in physics, but sometimes it is the breaking of symmetry that reveals the true structure of a system. Think of a crystal forming from liquid: the molecules are free to move in the liquid, but once they freeze into a lattice, symmetry is lost, and order appears.
The new tensor network method takes advantage of this principle. By mapping systems to symmetry-breaking ground states, the researchers eliminated unnecessary computational overhead. The result was a far more efficient way to simulate the low-energy behavior of many-body quantum systems, without sacrificing accuracy.
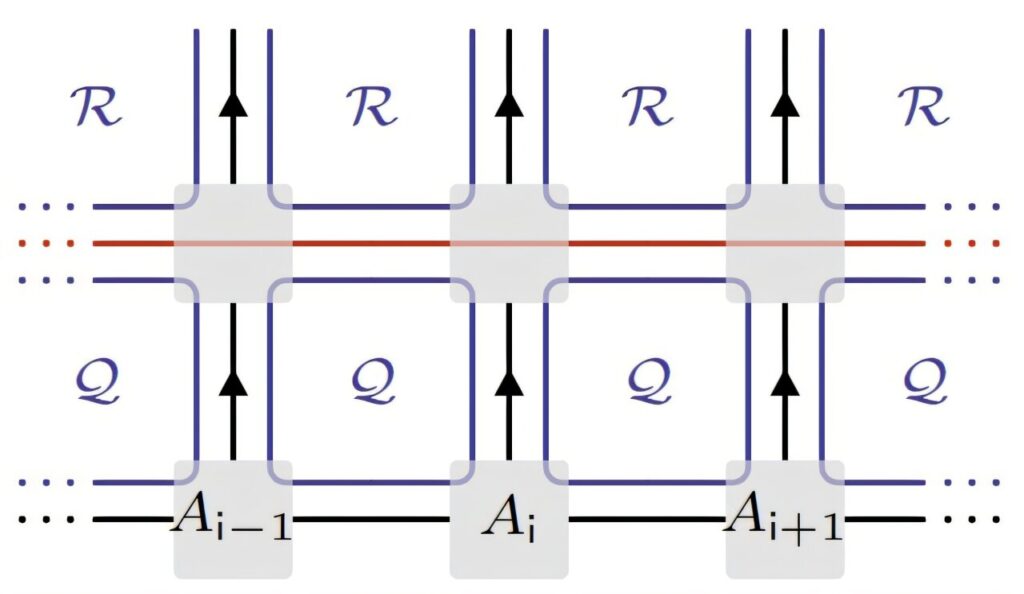
This approach also allowed the team to extract information about quasiparticle excitations—disturbances that ripple through quantum materials like waves across water. In condensed matter physics, understanding these excitations is essential for predicting how materials conduct electricity, respond to magnetic fields, or even store quantum information.
One-Dimensional Today, Higher Dimensions Tomorrow
For their initial work, the team applied their method to one-dimensional quantum spin chains. These systems, while mathematically simpler, still capture many essential features of quantum many-body physics. They serve as a testbed for ideas that can later be extended to higher dimensions, where the real challenges—and opportunities—lie.
Higher-dimensional many-body systems are notoriously difficult to simulate. The computational cost skyrockets, and existing tensor network methods struggle to keep up. But by generalizing their symmetry-based approach, the researchers believe they can make progress in tackling two- and three-dimensional problems. Such advances could unlock insights into quantum phases of matter that remain largely mysterious today.
The Broader Impact of the Work
The implications of this research stretch far beyond academic curiosity. Accurately simulating quantum many-body systems is central to the development of quantum technologies. Quantum materials could enable lossless power transmission, ultra-sensitive detectors, or revolutionary new forms of computation.
By combining deep mathematics with innovative computational techniques, this new framework represents a step toward making the intractable tractable. It also highlights an ongoing trend in physics: the blending of once-separate fields. Ideas from quantum information theory, abstract algebra, and condensed matter physics now flow together, creating new tools for understanding the quantum world.
Toward the Future of Quantum Simulation
The quantum many-body problem remains one of the great frontiers of science. It challenges not only our computational abilities but also our conceptual understanding of emergence, order, and complexity in the quantum realm. Yet progress is accelerating. With methods like tensor networks enriched by generalized symmetries, physicists are gaining a clearer view of the quantum landscape.
The vision is bold: to simulate, predict, and ultimately harness the collective power of quantum particles. In doing so, researchers may not only answer fundamental questions about nature but also unlock technologies that reshape the future.
The journey is far from over, but each advance—like the one pioneered by the Cambridge, IHES, and Ghent team—brings us closer to turning the impossible into the possible. In the strange but beautiful world of quantum many-body physics, the adventure of discovery has only just begun.
More information: Laurens Lootens et al, Entanglement and the density matrix renormalization group in the generalized Landau paradigm, Nature Physics (2025). DOI: 10.1038/s41567-025-02961-2