Physics is the science that seeks to describe the natural world with precision. Whether you’re studying the motion of planets or the flow of electricity through a wire, physics provides the language and the mathematics to interpret and predict behavior in the universe. But before we can dive into advanced theories or equations, we must understand some of the most fundamental concepts that form the backbone of this discipline. Two such foundational ideas are scalars and vectors.
These terms might sound like dry definitions from a textbook, but in reality, they are essential to how we interpret everything from throwing a ball to launching a rocket. They define how quantities behave, how they are manipulated mathematically, and how they interact with one another. Grasping the distinction between a scalar and a vector is not just academic—it’s a doorway into the deeper beauty of physics itself.
In this article, we will explore the differences between scalars and vectors, delve into how they manifest in the physical world, examine their mathematical representations, and discuss why these differences matter. Prepare for a deep dive into one of physics’ most vital distinctions—an exploration that might change how you look at motion, energy, and even reality itself.
The Scalar: Simple, Yet Powerful
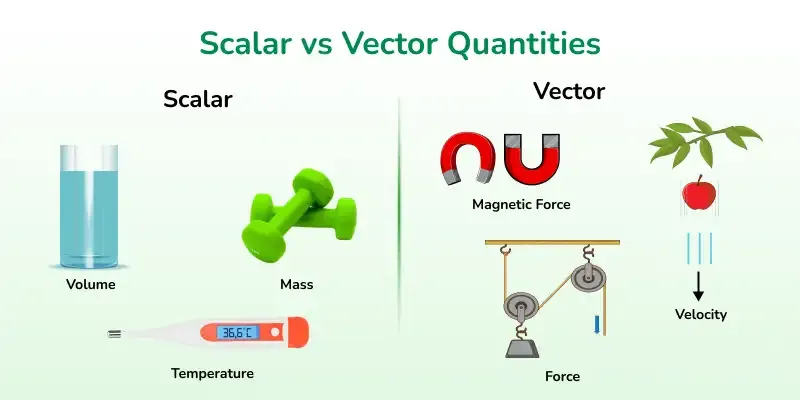
Let us begin with the simpler of the two: the scalar. A scalar is a quantity that has magnitude only. In layman’s terms, it’s something you can measure with a single number and unit. Scalars do not care about direction. They are concerned solely with “how much” or “how big.”
Temperature is a scalar. If you say it’s 30 degrees Celsius, you’ve provided a complete piece of information. There’s no direction associated with temperature; it’s just a measure of thermal energy.
Speed is another scalar. If a car is moving at 60 kilometers per hour, we know how fast it’s going, but not where. Volume, mass, energy, and time are all scalars, too. Each of these can be completely described by a single numerical value.
Despite their simplicity, scalars are indispensable. They form the quantities you add up, compare, or plug into equations in many branches of science. Their mathematical behavior is also straightforward—adding scalars simply means summing their values.
Yet, while scalars are everywhere, they are only part of the story. They tell us how much, but not in which direction. That’s where vectors come in.
The Vector: Direction Makes All the Difference
A vector is fundamentally different from a scalar because it possesses both magnitude and direction. This added feature—direction—makes vectors more complex, but also far more informative.
Take velocity, which is often confused with speed. Speed tells you how fast something is moving, but velocity tells you both how fast and in which direction. For instance, saying a plane is flying at 600 kilometers per hour is incomplete. But if you say it’s flying at 600 km/h northeast, you have a full vector quantity: both magnitude and direction.
Force is another vector. Push a book to the right across a table, and you apply a force with both a size (measured in newtons) and a direction. Acceleration, momentum, and displacement are also vector quantities.
Vectors are visually represented as arrows. The length of the arrow shows the magnitude, and the arrowhead points in the direction. This visual tool becomes incredibly useful when multiple vectors interact—such as when combining wind direction with an airplane’s heading, or analyzing forces acting on a bridge.
In contrast to scalars, vectors require special mathematical handling. Adding vectors involves not just simple arithmetic but also geometry, trigonometry, and sometimes calculus. Yet this complexity allows vectors to model the real world with much greater fidelity.
A Real-World Comparison: Walking Through Scalars and Vectors
Imagine you’re standing at a starting point and walk 5 kilometers north. This displacement is a vector—it tells both how far you went and in what direction. Now suppose you walk another 5 kilometers south. Your total distance traveled is 10 kilometers—a scalar. But your net displacement? Zero kilometers. You’re right back where you started.
This simple example illustrates why direction matters. Scalars like distance don’t change based on direction. Vectors, however, are deeply tied to direction and therefore can cancel each other out even when magnitudes are high.
This principle becomes crucial in understanding navigation, engineering, and any system involving multiple interacting forces. It’s why a pilot needs to know not just wind speed (a scalar) but wind velocity (a vector). It’s why structural engineers calculate not just how heavy something is, but how and where that weight is applied.
Mathematical Representation: Coordinates, Components, and Operations
To work with vectors effectively, we represent them mathematically, often using Cartesian coordinates. In a two-dimensional space, a vector might be written as v = (vx, vy), where vx is the component along the x-axis and vy is the component along the y-axis.
Suppose you’re moving northeast with a velocity of 10 m/s at a 45-degree angle. Using trigonometry, this can be broken down into:
vx = 10 * cos(45°)
vy = 10 * sin(45°)
This results in approximately (7.07 m/s, 7.07 m/s). Now, instead of thinking of motion in a general direction, we have precise components that can be independently analyzed.
Vector operations include addition, subtraction, scalar multiplication, and dot and cross products. Each operation reveals different aspects of how vectors interact.
Adding vectors involves summing their components. If vector A = (3, 4) and vector B = (1, 2), then A + B = (4, 6). This corresponds to placing the tail of one vector at the head of another and drawing a new vector from the origin to the new head position.
Subtraction works similarly, allowing us to determine relative motion or displacement. Multiplying a vector by a scalar scales its length but does not change its direction, much like turning up the speed of a car without changing where it’s headed.
Dot and cross products introduce deeper ideas. The dot product of two vectors gives a scalar and tells you how much one vector lies in the direction of another. The cross product gives another vector and is used extensively in physics to determine things like torque and magnetic force.
Scalars in Equations: The Unassuming Power Players
Even though scalars don’t have direction, they often play key roles in vector equations. For instance, when you multiply a vector by a scalar, you’re scaling its magnitude without altering its direction.
Consider Newton’s second law of motion: F = ma. Here, force (F) is a vector, mass (m) is a scalar, and acceleration (a) is a vector. The scalar mass simply scales the acceleration vector, giving a force vector in the same direction as the acceleration.
Energy equations also rely heavily on scalars. Kinetic energy is given by KE = ½mv², a scalar quantity derived from mass and speed (itself the scalar magnitude of velocity). Even when vectors are involved, the resulting quantity can be scalar, depending on the operation used.
This interplay between scalars and vectors in physics is a delicate balance. Scalars may lack direction, but they are often the coefficients, constants, and parameters that shape vector behavior.
Vectors in Action: From Orbits to Engineering
The utility of vectors comes alive in applied physics. Consider planetary motion. Newton’s law of universal gravitation describes a force between two masses, but it’s the vector form that allows us to determine not just how strong that force is, but in which direction it pulls.
In engineering, stress and strain are vector and tensor quantities. You can’t just know how much force is acting on a structure—you must know the direction and point of application. Otherwise, buildings might buckle, bridges might fail, and airplanes might crash.
In electromagnetism, vectors become essential. Electric and magnetic fields are vector fields; they have different strengths and directions at different points in space. Maxwell’s equations, the cornerstone of electromagnetic theory, are vector equations that describe how these fields propagate, interact, and give rise to phenomena like light.
Even in everyday life, vectors sneak in. The GPS in your phone calculates vector displacements to guide you. Weather maps show wind vectors to forecast storms. Video games use vectors for motion, collision detection, and physics simulations.
Scalars and Vectors in Relativity and Quantum Physics
In Einstein’s theory of relativity, scalars and vectors evolve into more complex entities. Time, for instance, is a scalar in classical physics. But in special relativity, time becomes intertwined with space to form spacetime—a four-dimensional vector-like entity called a four-vector.
Velocity in relativity is no longer simply distance over time but must be transformed according to relativistic rules. Scalars like mass also become frame-dependent; the concept of “relativistic mass” emerges, where mass increases with velocity.
Quantum mechanics adds further layers. The wave function, central to quantum theory, is a complex scalar field—each point in space and time has an associated complex number. However, observables like momentum and angular momentum remain vector quantities, and their behavior is governed by operator algebra in vector spaces called Hilbert spaces.
Even in this abstract mathematical landscape, the distinction between scalar and vector remains foundational. It affects how particles interact, how waves propagate, and how we understand the probabilistic nature of the universe.
Beyond Vectors: Tensors and Fields
As physics advances, scalars and vectors prove insufficient for certain applications. Enter tensors, which are generalizations of vectors. A scalar is a rank-0 tensor, a vector is a rank-1 tensor, and more complex interactions—like stress in three dimensions—require rank-2 tensors.
Tensor calculus is the language of general relativity. The curvature of spacetime itself is described using a tensor called the Riemann curvature tensor. This mathematical object encapsulates how mass and energy distort spacetime, producing what we perceive as gravity.
Field theory also builds on vectors. A scalar field assigns a scalar value to every point in space (like temperature), while a vector field assigns a vector to every point (like wind velocity). These fields interact, evolve, and obey laws that are the bedrock of classical and modern physics.
Teaching the Next Generation: Intuition and Visual Learning
Understanding the scalar-vector distinction is often a student’s first foray into mathematical physics. Yet, it can be an abstract hurdle. Educators increasingly use visual aids, interactive simulations, and real-world analogies to make the concepts intuitive.
Seeing vectors as arrows, manipulating them on screen, and observing how they add or cancel helps develop a visceral understanding. Connecting these concepts to real phenomena—throwing a basketball, sailing a boat, riding a bike—bridges the gap between theory and lived experience.
When students grasp not just the definition, but the why behind scalars and vectors, a deeper appreciation for physics follows. They begin to see the world not just as a collection of numbers, but as a dynamic system governed by elegant rules.
Conclusion: Direction, Magnitude, and Meaning
Scalars and vectors may appear at first to be simple classifications, but they are the lens through which physics views the universe. They dictate how we model motion, energy, forces, and fields. Scalars give us the magnitude; vectors give us both magnitude and direction. Together, they form the vocabulary of physical law.
Whether you are calculating how fast a car is moving or unraveling the equations that describe black holes, these two concepts will always be at your side. They are the first step toward understanding a cosmos that is complex, beautiful, and astonishingly structured.
And so, when you next hear the terms “scalar” and “vector,” don’t dismiss them as dry jargon. They are the keys to unlocking motion, change, and reality itself—silent pillars of the physical world.