Power. The word conjures up images of strength, dominance, and force. We speak of powerful engines, powerful leaders, powerful emotions. But in physics, power has a very precise and elegant definition. It’s not about how strong something is, or even how much work it can do, but how fast that work is done. Power is the rate at which work is performed or energy is transferred.
This may sound simple, but the implications of this concept stretch across the cosmos—from the fiery hearts of stars to the tiny motors in our phones. Understanding power is key to unlocking everything from how your car engine works to why the sun shines. It’s the bridge between raw energy and time, the tempo at which the universe operates.
Let’s take a deep and fascinating dive into the concept of power in physics, breaking it down into its core principles, unraveling the math behind it, examining its many real-world applications, and seeing how it shows up in surprising places—from lightning bolts to Olympic sprinters.
The Fundamental Concept: Defining Power
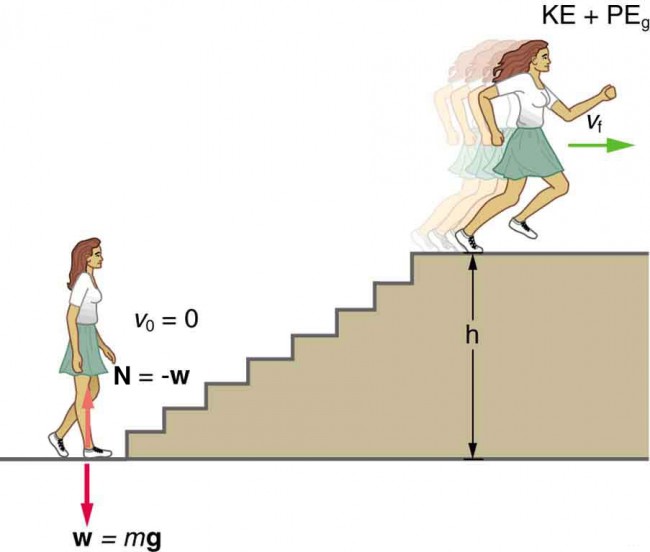
To grasp power, we first need to understand a fundamental concept in physics: work. In everyday life, “work” might mean sending emails, lifting weights, or digging holes. But in physics, work has a strict definition: it is the process of a force causing a displacement. Mathematically, work (W) is the product of force (F) and displacement (d), as long as the force is applied in the direction of the displacement:
W=F⋅d⋅cos(θ)W = F \cdot d \cdot \cos(\theta)
Where θ is the angle between the force and the displacement vectors.
Now, power enters the scene when we ask: how quickly is this work being done? That’s where we define power (P) as the rate at which work is done or energy is transferred:
P=WtP = \frac{W}{t}
Here, W is work (in joules), and t is time (in seconds). The unit of power in the International System of Units (SI) is the watt (W), named after Scottish inventor James Watt, a key figure in the development of the steam engine. One watt is equal to one joule per second.
A Tale of Two Sprinters: Power in Motion
Let’s put this into context. Imagine two sprinters running a 100-meter race. Sprinter A finishes in 10 seconds, while Sprinter B finishes in 12 seconds. Suppose both expend the same amount of energy to complete the race. Which one has more power?
The answer is clear: Sprinter A. Though the work done is the same (both moved the same mass—their bodies—the same distance), Sprinter A did it in less time. That means their power output was greater. In essence, power measures not just what gets done, but how fast it gets done.
This distinction is vital. A person slowly lifting a box off the ground might do the same amount of work as someone who hurls it skyward, but the latter does so with greater power.
Mechanical Power: Engines, Gears, and Machines
In engineering and mechanics, power takes on a practical dimension. Consider a car engine. When you hear that a vehicle has “200 horsepower,” you’re hearing a measure of power—specifically, how fast the engine can do work. Horsepower, by the way, is an old unit of power where one horsepower equals about 746 watts. It was devised by James Watt to compare the output of steam engines to draft horses.
Engineers calculate mechanical power using variations of the basic formula. If an object is moving at a constant velocity, and a force is being applied to keep it moving (overcoming friction or air resistance, for instance), power can also be expressed as:
P=F⋅vP = F \cdot v
Where F is force and v is velocity. This tells us how much power is required to maintain motion at a given speed against a resisting force.
In machines, the goal is often to increase power efficiency—how much useful power you get out compared to how much energy you put in. Gears, pulleys, and levers are all ways to manage the flow of force and motion, and thus power.
Electrical Power: The Heartbeat of Modern Civilization
While mechanical power might move wheels and gears, electrical power lights up our cities and charges our devices. In electrical systems, power can be expressed in terms of current (I) and voltage (V):
P=V⋅IP = V \cdot I
This is the power consumed by a circuit element, such as a lightbulb or a motor. The more current flows through, and the higher the voltage pushing it, the more power is used.
Electrical power can also be dissipated as heat. Consider a toaster. Electrical energy flows in, heating elements resist the flow (creating heat), and soon you’re munching on a slice of toast. That’s power at work—quite literally—turning electrons into breakfast.
Alternating current (AC) systems, which power most of our homes, involve a more complex understanding of power, including concepts like real power, apparent power, and reactive power. Real power (measured in watts) does actual work. Reactive power (measured in VARs—volt-ampere reactive) doesn’t do work but is necessary to maintain voltage levels. Apparent power (measured in volt-amperes) combines both.
Human Power: The Physics of Performance
Let’s return to the human body for a moment. Your muscles, in essence, are biological engines. They convert chemical energy (from food) into mechanical energy (movement). But how much power can a human produce?
The answer varies. A well-trained cyclist might sustain 400 watts of power over an hour. A sprinter might generate over 2,000 watts briefly at peak effort. For comparison, a typical incandescent lightbulb uses about 60 watts. So, even when you’re jogging lightly, your body is producing enough power to light up a room.
Power in biological systems is about balance. Muscles must generate force quickly, efficiently, and sustainably. Too much force too fast, and you risk injury. Too slow, and you lose performance. Training, diet, and recovery all influence your body’s ability to produce power.
Power and Energy: A Crucial Distinction
One of the most common confusions in physics—and in everyday life—is the difference between power and energy. They are related, but not the same.
Energy is the capacity to do work. It’s stored in fuels, batteries, springs, and even food. It’s measured in joules, calories, kilowatt-hours, and more. Power, as we’ve said, is the rate at which that energy is used.
Think of energy as money, and power as how quickly you spend it. A 100-watt light bulb uses energy at a rate of 100 joules per second. If it runs for one hour, it consumes 100 watts × 3600 seconds = 360,000 joules, or 0.1 kilowatt-hours.
This distinction is crucial in everything from power plant design to your monthly utility bill. You pay for energy (kWh), but the appliances and devices you use have power ratings (watts).
Power in Nature: Storms, Stars, and Supernovas
Nature, too, is full of stunning displays of power. A lightning bolt can unleash over a billion joules of energy in a fraction of a second—equating to a power output of several billion watts. The sun, meanwhile, radiates energy at a staggering rate of about 3.8 × 10²⁶ watts. That’s 380,000,000,000,000,000,000,000,000 watts—every second.
When a star explodes in a supernova, it can briefly outshine an entire galaxy, releasing more power in a few seconds than the sun will in its entire lifetime. These cosmic events are the ultimate expressions of power in the universe, demonstrating both its might and its fleeting nature.
Even on Earth, consider earthquakes and volcanoes. The energy released in these events occurs rapidly—hence the immense power involved. Understanding the power of natural disasters helps scientists predict and prepare for their impact.
Power Efficiency: Doing More With Less
Power efficiency is a measure of how well a system converts energy into useful work. A car engine, for example, might convert only 25-30% of the chemical energy in gasoline into motion—the rest is lost as heat. An electric motor, on the other hand, might achieve 90% efficiency.
In our energy-hungry world, improving power efficiency is a central concern. Engineers work tirelessly to design machines, systems, and technologies that do more work with less energy—and less waste. From LED lighting to hybrid cars to renewable energy systems, efficiency is key.
In physics, the efficiency η (Greek letter eta) is defined as:
η=Useful Power OutputTotal Power Input\eta = \frac{\text{Useful Power Output}}{\text{Total Power Input}}
A system with η = 1 (or 100%) would be perfectly efficient—no energy lost. In reality, all systems lose some energy, often as heat, sound, or vibration.
Instantaneous and Average Power
In real-world systems, power often fluctuates. A blender doesn’t use the same amount of power every millisecond. That’s why physicists distinguish between average power and instantaneous power.
Average power is calculated over a period of time:
Pavg=ΔWΔtP_{\text{avg}} = \frac{\Delta W}{\Delta t}
Instantaneous power, on the other hand, is the power at a specific moment, and can be calculated using calculus:
P=dWdtP = \frac{dW}{dt}
Or, in terms of force and velocity:
P=F⃗⋅v⃗P = \vec{F} \cdot \vec{v}
This distinction is crucial in analyzing systems where power varies rapidly, such as audio amplifiers, car engines, or even biological muscles under load.
Measuring Power: Tools of the Trade
Power measurement depends on the system. Mechanical power is often measured with devices like dynamometers, which assess the force and rotational speed of engines. Electrical power is measured with wattmeters, ammeters, and voltmeters, using the relationship between current, voltage, and resistance.
In more complex systems, like power grids, engineers use sophisticated sensors and software to monitor power flow, detect losses, and manage distribution. These measurements are critical in balancing supply and demand and ensuring grid stability.
Even in the body, scientists can estimate metabolic power through measurements of oxygen consumption, heart rate, and mechanical output during exercise. Sports scientists use these tools to optimize athletic performance and prevent injury.
Power in Relativity and Quantum Mechanics
Even in the abstract realms of modern physics, power has a place. In special relativity, energy and time are deeply linked, and power must be calculated with care when speeds approach that of light. The relativistic energy-momentum relation changes how we think about work and motion.
In quantum mechanics, power isn’t often used directly, but the principles of energy transfer, time evolution, and rates of change underpin many quantum processes. Lasers, for instance, are judged by their output power, which relates to the rate of photon emission. Even radioactive decay involves a kind of power, as energy is released over time.
Conclusion: The Pulse of Physical Reality
Power is everywhere. It’s in the muscles that lift, the engines that roar, the currents that flow, and the stars that shine. It measures how quickly the universe moves its energy around—how fast work gets done, whether by a sprinter’s legs or a black hole’s gravity.
Understanding power gives us insight into efficiency, performance, safety, and sustainability. It tells us how to build better machines, design smarter cities, and even comprehend the vast, churning cosmos.
In physics, power is not just a number—it’s a story about time, change, and motion. It reminds us that doing work is important, but doing it with speed and purpose is what truly shapes our world.