For centuries, poets, artists, and lovers have been captivated by the rose—an emblem of beauty, romance, and mystery. Its tightly coiled petals unfurl into spirals of breathtaking symmetry, its fragrance a whisper from nature’s secret garden. But beneath the elegance and symbolism lies a question no one had fully answered: how does a rose blossom into its complex and exquisite shape? Now, four physicists from the Hebrew University of Jerusalem have unveiled the mechanical mystery behind this iconic floral bloom.
In a groundbreaking study published in Science, researchers Yafei Zhang, Omri Cohen, Michael Moshe, and Eran Sharon applied the rigor of theoretical physics, computational modeling, and hands-on experimentation to understand the physical forces and geometric principles driving the formation of rose petals. Their discovery goes far beyond botany—it opens new doors into material science, bio-inspired design, and the fundamental mathematics that shape living forms.
A Blooming Mystery Meets Physics
Despite their enduring place in human culture, roses had not been deeply studied from a physical or geometric perspective. Botanists understood the cellular and genetic pathways that govern petal development, but the question of form—why a rose looks like a rose—had not been answered with the language of mechanics. What makes a rose’s petals curl in those distinctive overlapping spirals, with sharp creases and gentle folds that seem both chaotic and perfectly ordered?
The Hebrew University team decided to address this mystery not by looking inside the cell, but by zooming out to the level of geometry, stress, and physical constraints. In doing so, they entered the world of geometric incompatibility, a subtle but powerful concept in physics and materials science.
The Three-Tiered Approach: Theory, Simulation, and Synthetic Petals
To decode the blossoming process, the researchers adopted a three-pronged method.
First, they began with theoretical analysis. Using the principles of differential geometry and elasticity theory, they explored how a thin, flexible sheet—like a petal—responds to growth forces. Their equations revealed a crucial insight: when a surface tries to grow into a shape that violates the conditions of geometric compatibility, internal stresses arise. These stresses don’t just distort the surface—they sculpt it.
Next, they moved to computer simulations. By creating digital models of petals under realistic growth conditions, they could watch virtual roses blossom in slow motion. The simulations allowed the team to tweak parameters—such as the rate of growth or the curvature of the petal base—and observe how these changes affected the petal’s final form. It was a way to play god in silico, generating endless variations on the theme of the rose.
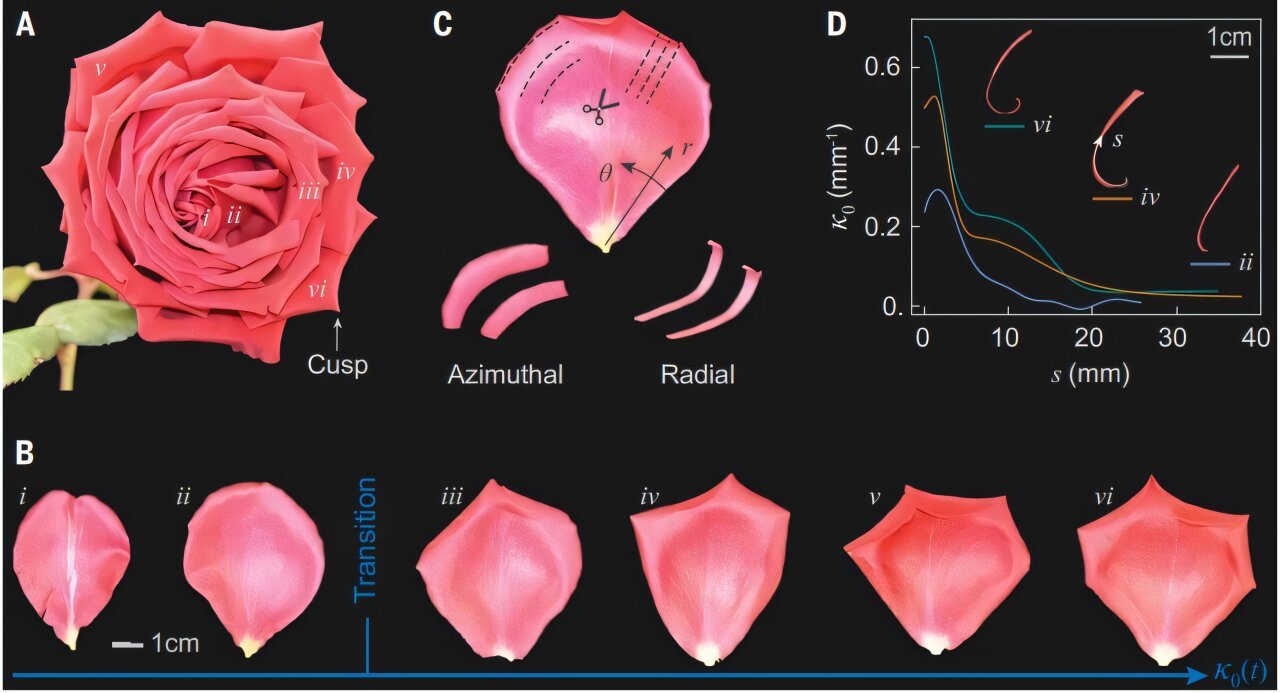
Finally, they brought their models to life using physical prototypes. They created bendable plastic disks designed to mimic the mechanical properties of rose petals. As the plastic “petals” expanded, they began to curl, twist, and crease—replicating the forms seen in real rose blossoms. These synthetic flowers became a bridge between theoretical physics and the living garden.
Mainardi-Codazzi-Peterson: The Frustration That Shapes a Rose
The heart of their discovery lies in a phenomenon known as Mainardi-Codazzi-Peterson incompatibility. It’s a mouthful of a name, but its role is deceptively simple: it’s the frustration that arises when a growing surface cannot satisfy the geometric conditions that define a smooth, continuous shape.
In ideal conditions, a growing petal might simply curve into a shallow, dish-like form. But the Mainardi-Codazzi-Peterson conditions impose constraints that the rose cannot fulfill during its real-life growth. As a result, stress builds up in the petal’s surface—tension and compression pushing and pulling at each other like tectonic plates beneath the Earth’s crust. The petal, seeking release, forms sharp cusps and multiple curls, each a signature of geometric incompatibility.
In other words, the petal doesn’t choose its shape—the shape is forced upon it by physics. The creases and folds we admire in a rose are the result of mathematical constraints and the petal’s elegant negotiation with those constraints.
Roses vs. Other Flowers: A Unique Morphological Path
Interestingly, the study reveals that roses are distinct from most other flowers in how they resolve these geometric stresses. Many flowers, when subjected to growth stresses, show what’s known as Gauss incompatibility. In these cases, the surface deforms in soft, wavy patterns without sharp edges or high curvature. Think of the gently undulating petals of a daffodil or tulip—they lack the crisp creases and curled lobes of a rose.
The rose, however, is a rebel. Under the influence of Mainardi-Codazzi-Peterson incompatibility, it takes a different path. It accumulates stress until it can no longer grow smoothly, and then it snaps into a new configuration—marked by sharp curves and well-defined ridges. These features aren’t just aesthetic flourishes—they are mechanical artifacts, physical expressions of frustrated growth.
This insight elevates our appreciation of the rose’s form. It is not merely beautiful—it is inevitably beautiful, shaped by deeper forces than DNA alone.
Beyond the Garden: Applications in Material Science
While the study sheds light on one of nature’s most beloved flowers, its implications stretch far beyond the rose garden.
Understanding how growth-induced stress creates form is central to soft robotics, bio-inspired design, and shape-morphing materials. Engineers can use the principles uncovered in this research to design flexible materials that change shape predictably under stress, or to create programmable surfaces that mimic natural forms. Just as roses form intricate patterns from uniform growth, future technologies might use geometric incompatibility to self-assemble into complex devices.
Furthermore, the work has potential applications in tissue engineering and biomechanics, where scientists try to grow or mimic organic tissues that undergo large shape changes—like arteries, skin, or even leaves. Knowing how nature handles incompatible growth gives us a blueprint for guiding similar behavior in synthetic systems.
The Geometry of Living Art
In the accompanying Perspective article in Science, Qinghao Cui and Lishuai Jin from the University of Hong Kong praised the Hebrew University team for their multidisciplinary approach. They noted that the study offers a compelling example of how physics and biology intertwine—how the language of curvature and constraint can explain the exquisite artistry of nature.
The rose, in this view, is more than a flower. It is a geometric sculpture, carved not by human hands but by the slow and inevitable logic of physical laws. It is a living proof that elegance can emerge from stress, and that beauty can be born from frustration.
A Flower in a New Light
We often take the beauty of a rose for granted. We admire its fragrance, its symmetry, its softness—but now we can admire its mathematical precision, too. Thanks to the work of Zhang, Cohen, Moshe, and Sharon, we see the rose not only as a symbol of love or a subject for art, but as a textbook of physics, blooming on a stem.
It is a reminder that nature’s patterns are not random, but rule-bound. That what we perceive as effortless grace is, in fact, the product of relentless negotiation with geometry and force. The rose has always inspired us—but now, it challenges us too: to see the science in the sublime, and to recognize the laws of the universe not only in the stars above, but in the petals beneath our fingertips.
References: Yafei Zhang et al, Geometrically frustrated rose petals, Science (2025). DOI: 10.1126/science.adt0672. www.science.org/doi/10.1126/science.adt0672
Qinghao Cui et al, The mechanics behind the beauty of roses, Science (2025). DOI: 10.1126/science.adx1733. www.science.org/doi/10.1126/science.adx1733