Quantum computers have often been described as the future of computation, holding the potential to solve problems that would take today’s most powerful supercomputers millions of years. Instead of relying on traditional bits that can only exist as 0 or 1, quantum computers use qubits—units of information that can exist in a superposition of states, meaning they can be 0 and 1 at the same time. Even more fascinating, qubits can become entangled, creating deep correlations that lie at the heart of quantum processing power.
But as groundbreaking as this sounds, making quantum computers practical is anything but straightforward. At the center of this challenge lies the quantum logic gate, the fundamental building block of quantum computation. These gates manipulate qubits, much like classical logic gates (AND, OR, NOT) operate on bits in traditional computers. Among them, two-qubit gates are especially important because they allow qubits to interact and become entangled. Without these interactions, quantum computers would be little more than sophisticated calculators.
Yet, despite their importance, building reliable two-qubit gates has remained one of the most difficult tasks in the field.
The Challenge of Two-Qubit Gates
Most existing methods for creating two-qubit gates require qubits to step outside their most stable operating conditions. Imagine trying to play a violin piece but being forced to constantly retune the strings mid-performance—the result is both inefficient and error-prone. Similarly, when qubits are pushed away from the conditions where they store and process information most reliably, they are more likely to “leak” into unwanted states, degrading the accuracy of the computation.
For decades, one gate has served as the workhorse of quantum computing: the CNOT (controlled NOT) gate. While essential, relying too heavily on one type of gate is a bit like trying to build a symphony with only a single instrument. Researchers have long suspected that the quantum world has more to offer.
A Breakthrough from Beijing and Tsinghua
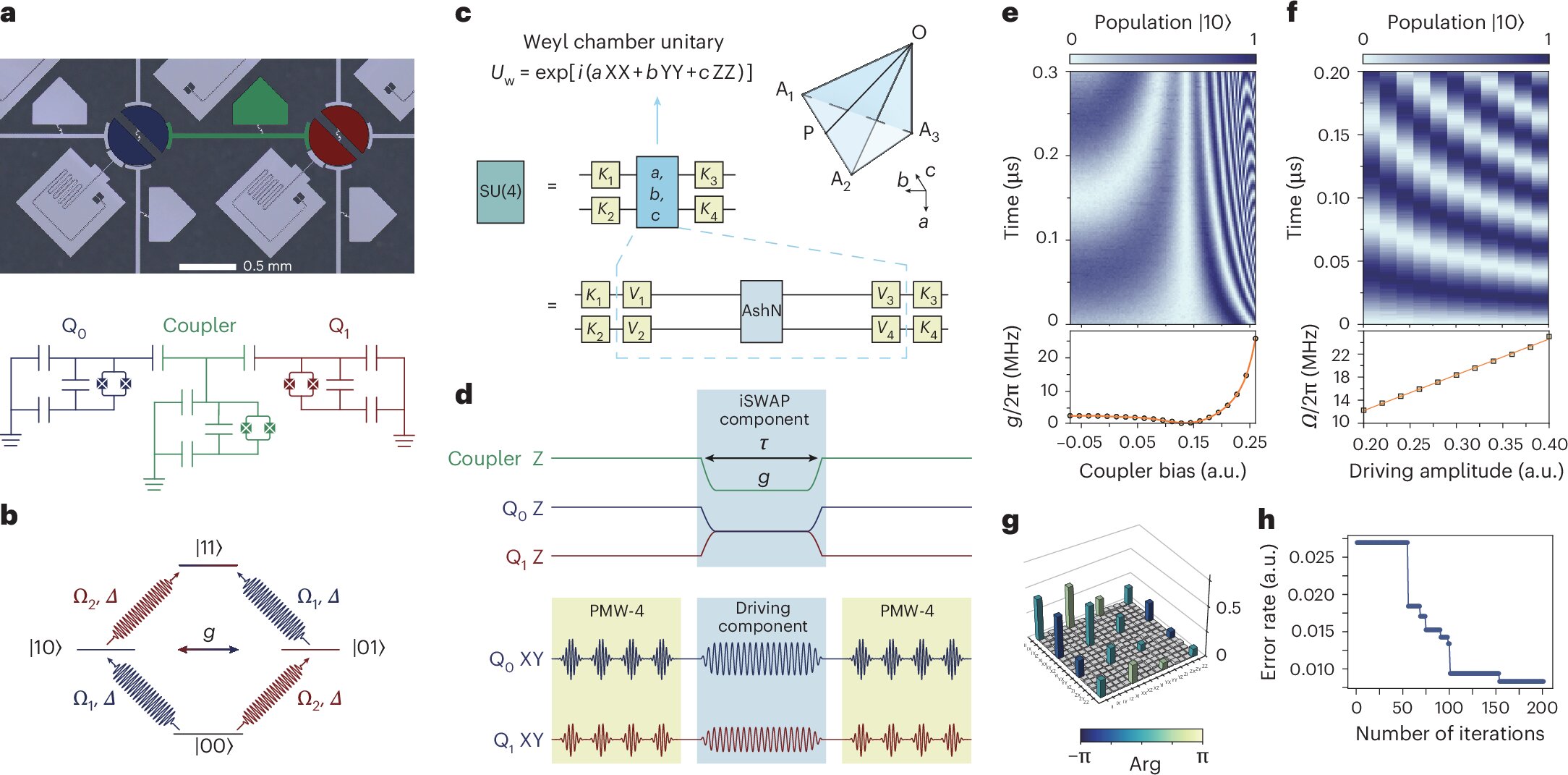
A team of researchers at the Beijing Academy of Quantum Information Sciences (BAQIS) and Tsinghua University has now taken an important step forward. In a study published in Nature Physics, they introduced a universal control scheme that allows superconducting quantum processors to implement any two-qubit gate with high fidelity.
This new approach is a significant leap because it breaks free from the reliance on a single gate type and instead embraces the entire family of possible two-qubit operations. Mathematically, this means their scheme supports all transformations within SU(4)—the complete set of valid two-qubit gates. In simpler terms, the researchers have shown a way to create a universal “instruction set” for quantum computers, one that doesn’t force qubits to work outside of their most natural conditions.
Rethinking Quantum Instructions
One of the most compelling insights of this research is the comparison to classical computing. Just as traditional processors are defined by their instruction set architecture—the basic set of operations they can perform—quantum computers may benefit from broadening their own instruction sets. By expanding the range of “native” two-qubit gates that can be implemented reliably, researchers can design faster, more efficient, and more error-resistant quantum algorithms.
Historically, quantum computing textbooks and laboratories emphasized the CNOT gate as the go-to tool. But as co-senior author Jianxin Chen explained, the field has recently recognized that a far wider variety of gates—such as the square root of iSWAP, fSim, and fractional gates—can be not only possible but also advantageous. The BAQIS–Tsinghua team’s scheme makes this expanded toolkit a reality.
How the Scheme Works
The researchers achieved this universality by combining two complementary approaches:
- Direct Qubit Interaction (Exchange Interaction): This method lets qubits interact naturally with one another, enabling entanglement without forcing them into unstable conditions.
- Microwave Control: Qubits are also steered using carefully designed microwave signals. This approach is compatible with the superconducting quantum hardware already being used in laboratories worldwide, which means it doesn’t require an overhaul of existing systems.
The result is a control framework that can implement any desired two-qubit gate using the same hardware configuration. Even more importantly, this method avoids one of the biggest pitfalls of older schemes: reliance on the |11⟩–|20⟩ transition, which frequently caused leakage into higher energy states. Instead, their method operates solely within the |01⟩–|10⟩ transition, a safer and more stable pathway.
Why This Matters for Quantum Error Correction
Quantum error correction is one of the biggest hurdles in making quantum computers practical. Unlike classical bits, qubits are fragile and prone to decoherence—losing their quantum state due to interactions with the environment. Error correction codes, such as the surface code and qLDPC codes, are essential for stabilizing computations, but they demand extremely high-fidelity gates to work effectively.
By providing a method that minimizes leakage and ensures reliable two-qubit operations, the BAQIS–Tsinghua scheme could make quantum error correction easier to implement and more efficient. In fact, early studies suggest that this new approach could even help overcome some long-standing limitations of existing codes.
A Step Toward Quantum Advantage
The long-term goal of quantum computing is to achieve quantum advantage—the point at which a quantum computer can solve problems faster than any classical counterpart. Every innovation in gate design, error correction, and hardware stability brings this dream closer to reality.
The universal two-qubit gate scheme doesn’t just refine existing methods; it redefines what’s possible. By treating all two-qubit operations as equally valid and equally accessible, it opens the door to new algorithmic strategies, improved performance, and ultimately, more powerful quantum processors.
As Chen put it, this is not only about building better gates but also about “re-examining the boundaries of quantum advantage.”
The Road Ahead
The research is still in its early stages, and many challenges remain. Scaling up quantum computers to thousands—or millions—of qubits while maintaining precision will require continued breakthroughs in materials, design, and calibration. But the BAQIS–Tsinghua scheme represents a crucial step forward: a reminder that the path to quantum computing is not linear but full of creative rethinking and bold experimentation.
Future directions will likely include:
- Developing more efficient calibration schemes to fine-tune this universal approach.
- Integrating the method into larger-scale quantum processors.
- Exploring how different types of quantum algorithms can best take advantage of this expanded gate set.
Conclusion: Toward a New Quantum Era
Quantum computers are no longer just theoretical curiosities. They are steadily evolving into tools that could revolutionize industries from cryptography to drug discovery, from climate modeling to artificial intelligence. Yet their success depends on solving the fundamental challenge of controlling qubits with precision.
The BAQIS–Tsinghua team’s universal scheme for two-qubit gates is more than just a technical advance—it is a conceptual breakthrough. It tells us that instead of forcing quantum systems into awkward configurations, we can embrace their natural strengths. By doing so, we move closer to a world where quantum computers are not fragile prototypes but reliable engines of discovery.
In the end, quantum physics has always taught us that reality is richer and stranger than we first imagined. This new work reminds us of that truth once again: in the entanglement of qubits and the elegance of universal gates, we are beginning to glimpse the true power of the quantum world.
More information: Zhen Chen et al, Efficient implementation of arbitrary two-qubit gates using unified control, Nature Physics (2025). DOI: 10.1038/s41567-025-02990-x.