Picture this: a baseball bat slams into a fastball with a sharp crack, sending the ball hurtling over the outfield fence. The contact lasted mere milliseconds. Yet, in that brief moment, the ball’s momentum completely reversed, changing direction and speed dramatically. What exactly happened in those microseconds? How can such a short contact time result in such a powerful effect? The answer lies in a powerful, often overlooked concept in physics—impulse.
Impulse may not be as famous as force, energy, or momentum, but it is the bridge between motion and force, time and change. Impulse helps us understand not just the “what” of an event but the “how” and “why.” It’s what happens when a force is applied for a short amount of time, causing a sometimes radical shift in an object’s momentum. And it turns out, impulse is everywhere—from car crashes and airbags to tennis volleys, hammer swings, and rocket launches.
To fully appreciate impulse, we need to dive into the very essence of what makes things move and change. This is a journey into a rapid-fire dance of forces and time, a core principle of Newtonian mechanics that connects the abstract with the intensely physical.
Defining Impulse: A Quick Introduction
Impulse in physics is defined as the product of force and the time interval over which that force acts. In mathematical terms, it’s written as:
Impulse (J) = Force (F) × Time interval (Δt)
But this deceptively simple formula conceals a powerful truth: impulse is not just about how much force is applied, but for how long. A small force applied over a long period can have the same effect as a huge force applied in a flash. That’s where impulse gets interesting—it’s a game of balance between force and time.
Impulse has the same units as momentum (kilogram-meter per second, or kg·m/s), and that’s no accident. In fact, impulse is the thing that changes an object’s momentum. When we say something has experienced an impulse, we’re really saying it had its momentum altered by a force applied over a period of time.
This gives us the Impulse-Momentum Theorem:
Impulse (J) = Change in momentum (Δp)
Or in physics terms:
F × Δt = m × Δv
Where:
- F is the average force,
- Δt is the time the force acts,
- m is the mass,
- Δv is the change in velocity.
This theorem is the key that unlocks how motion changes in the real world, whether in sports, collisions, explosions, or even celestial dynamics.
From Theory to Touch: Feeling Impulse in Everyday Life
You might not realize it, but you experience impulse constantly. Think about slapping your hand on a table. If you do it quickly and forcefully, it stings. Now try slapping the table with the same hand, but gently and slowly increasing pressure until your palm is resting flat. What changed?
The total force over time—that is, the impulse—was very different. In the first case, the force was sharp and brief, causing a big change in your hand’s momentum in a short time. In the second, the force was small and prolonged, spreading the momentum change over a longer duration. That’s why it didn’t hurt.
Impulse becomes especially vivid in sports. When a soccer player kicks a ball, the brief moment of contact changes the ball’s motion instantly. A golf club transferring its momentum to a ball during a drive is a pure moment of impulse. The player doesn’t apply constant force over seconds—they apply a burst of force that quickly changes the ball’s momentum.
Even in something as mundane as driving, impulse shows up. Braking suddenly causes a large impulse as the car’s momentum decreases rapidly. If a crash occurs, safety features like airbags increase the time over which the force acts, reducing the average force experienced by the occupants. This is impulse in action—literally saving lives.
The Mathematics of Impulse: More Than a Formula
To truly understand impulse, we need to go deeper than just the formula. Let’s look at impulse not as a static number but as something dynamic, unfolding over time.
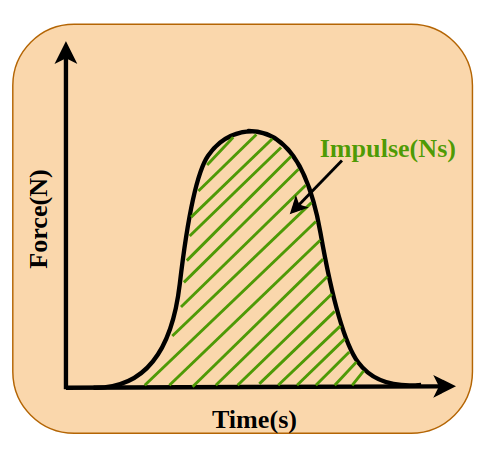
In physics, impulse can also be thought of as the area under the force-time curve. If you graph the force applied to an object on the y-axis, and time on the x-axis, the area under that curve gives you the impulse.
In many real-world cases, the force isn’t constant. Think about a boxer’s punch or a hammer strike. The force rises quickly, peaks, then falls off—all in less than a second. In such cases, calculating the average force times time gives you a rough estimate of impulse, but the actual value comes from integrating the force over time:
Impulse = ∫ F(t) dt
This perspective opens up a much more nuanced understanding. It means that impulse isn’t always a neat, single-value calculation. It depends on how the force varies with time, and that variation tells the story of the event.
Impulse and Momentum: Two Sides of the Same Coin
To understand impulse, we must revisit the concept of momentum. Momentum is the quantity of motion an object has. It’s given by:
Momentum (p) = mass × velocity (mv)
Momentum is conserved in a closed system, which means it doesn’t change unless acted on by an external force. Impulse is how that change happens.
So, impulse is not just a random change—it is the mechanism by which an external force alters an object’s momentum. That’s why we say impulse is the change in momentum:
Δp = J = F × Δt
This connection is more than academic. It underlies everything from orbital mechanics to crash test simulations. In fact, many physics problems involving collisions and rebounds are best solved using impulse and momentum, not force and acceleration.
Collisions: Where Impulse Rules the Game
Few places make the power of impulse more visible than collisions. Whether it’s cars crashing or pool balls clacking, collisions are moments of high-force, short-duration interaction—perfect conditions for impulse.
Let’s consider two bumper cars. When they collide, each exerts a force on the other for a very short time. During that micro-moment, both cars experience a change in momentum equal to the impulse delivered. Conservation of momentum governs the overall system, but impulse explains the mechanism of how that momentum changes.
There are two types of collisions: elastic and inelastic. In elastic collisions, objects bounce off each other, conserving both momentum and kinetic energy. In inelastic collisions, momentum is still conserved, but some kinetic energy is transformed into heat, sound, or deformation. In both cases, impulse tells us how the momentum of each object is altered.
Impulse also explains why padding is used in sports. Football players wear helmets not just to stop impact, but to lengthen the time over which the force is applied. This reduces the force by spreading it out—lower force, same impulse, safer player.
Airbags, Helmets, and Safety: Impulse Saves Lives
One of the most life-saving applications of impulse theory is found in safety engineering. Consider airbags in vehicles. When a car crashes, it stops suddenly, and without an airbag, the occupant would stop just as abruptly—experiencing a huge force in a very short time.
Airbags work by increasing the time over which your momentum decreases. Instead of hitting the dashboard in 0.02 seconds, you hit the airbag in 0.2 seconds. The impulse—the change in your momentum—is the same in both cases, but because the time is longer, the average force is dramatically reduced. That difference can mean the difference between life and death.
The same logic applies to motorcycle helmets, seatbelts, crash barriers, and even flooring in gyms. All of them work not by eliminating force, but by manipulating time—increasing it to reduce force for a given impulse. The physics is elegantly simple, but the effect is profoundly human.
Impulse in Sports: Power, Precision, and Timing
In sports, mastering impulse can be the difference between victory and defeat. Whether you’re swinging a bat, serving a tennis ball, or kicking a football, you’re generating an impulse to change the momentum of the object you’re hitting.
Take baseball. The force and timing of the bat determine the ball’s new velocity. A quick swing with high force delivers a greater impulse than a slower swing with less force. Coaches often talk about “follow-through” not just for style, but because it increases the contact time, boosting the impulse and sending the ball farther.
Tennis players use rackets designed to maximize impulse efficiency. A tighter string pattern or a heavier racket can deliver more impulse to the ball, changing its momentum faster. Golf clubs are engineered with specific mass distributions to optimize impulse transfer during the brief moment of impact.
Even in boxing, impulse is everything. The knockout punch isn’t just about strength; it’s about delivering a forceful impact in the shortest time. That’s impulse—using time and force together to maximize change in momentum.
Rockets and Thrusters: Impulse in Space
In the vacuum of space, where there’s no friction or air resistance, momentum becomes especially critical. So does impulse. When rockets fire, they don’t just push—they generate an impulse that changes their momentum.
Rocket engines produce thrust by expelling mass (exhaust gases) at high velocity. This expulsion creates an impulse on the rocket in the opposite direction—Newton’s third law in action. The longer the engine burns, and the greater the thrust, the larger the impulse and thus the greater the change in velocity.
Even in orbital adjustments, tiny thrusters deliver precise impulses to change a satellite’s momentum just enough to nudge it into a new orbit. In space exploration, impulse isn’t just a theory—it’s propulsion, navigation, and survival.
Negative Impulse: Slowing Things Down
Impulse isn’t always about speeding things up. It’s also about slowing down. When you catch a ball, your hands move backward to increase the time of contact, reducing the force. This is a negative impulse—one that decreases momentum.
The same principle applies when landing from a jump. Athletes bend their knees to absorb the impact over a longer period, reducing the force on their joints. The impulse remains the same, but how it’s distributed changes everything.
Negative impulses also appear in braking systems, parachutes, and re-entry vehicles. Space capsules deploy parachutes not just for show, but to increase the time over which they decelerate, reducing the destructive force of re-entry.
Impulse in Real-World Problems: Calculations in Action
Let’s consider a car crash scenario to see how impulse is calculated.
Suppose a car with a mass of 1000 kg is traveling at 20 m/s. It crashes into a wall and comes to a complete stop in 0.1 seconds. What is the impulse? What is the average force experienced?
First, calculate the change in momentum:
Δp = m × Δv = 1000 × (0 – 20) = -20,000 kg·m/s
This means the car experienced an impulse of -20,000 N·s (the negative sign indicates a reduction in velocity).
Now, to find the average force:
F = J / Δt = -20,000 / 0.1 = -200,000 N
That’s a massive force. But now imagine the same car has a crumple zone that extends the stop time to 0.5 seconds:
F = -20,000 / 0.5 = -40,000 N
The impulse is the same—the car still stops—but the force is five times smaller. That’s the life-saving difference of impulse management.
The Deeper Philosophy of Impulse: Change as a Product of Time
At a deeper level, impulse invites us to think differently about change. It reminds us that change doesn’t just depend on how strong a force is, but on how long it lasts. Time becomes a partner in transformation. Impulse is the marriage of force and time—a bridge between moments of impact and lasting motion.
In life, too, we often see dramatic changes happen not from constant pressure but from brief, powerful moments. A single word of encouragement, a moment of insight, or a flash of emotion—these are impulses in the human experience, changing our emotional or mental momentum.
In that sense, impulse is more than physics. It’s a metaphor for how small moments, applied with intensity, can shift the trajectory of an object—or a life.
Conclusion: The Power of a Moment
Impulse may be invisible, but its effects are felt in every fast change, every impact, every sudden stop or surge forward. It’s the silent driver behind collisions, athletic feats, technological marvels, and life-saving innovations.
Whether you’re a physicist modeling planetary motion, an engineer designing airbags, or a student tossing a basketball, understanding impulse unlocks a new layer of reality. It reveals how time and force, working together, shape the world in flashes of motion and moments of transformation.
So next time you see a tennis ball rocket off a racket, a skateboarder land a trick, or a spacecraft change course, remember: you’re witnessing impulse in action—the physics of change, condensed into the blink of an eye.