Chaos is a word that evokes fear, confusion, and unpredictability. In everyday life, chaos seems to mean disorder—traffic jams, financial crashes, turbulent weather, and unpredictable human behavior. Yet, beneath this apparent randomness lies a hidden order, a subtle structure that defies intuition. This is the essence of chaos theory: the study of complex systems whose behavior appears random but is governed by underlying patterns and rules. At first glance, it seems paradoxical. How can disorder hide order? How can something unpredictable follow rules? To understand this, we must step into a world where mathematics, nature, and imagination intertwine.
Chaos theory is not a modern invention; its seeds were planted centuries ago. Isaac Newton’s laws of motion and planetary dynamics suggested a deterministic universe, where knowing initial conditions could, in principle, allow perfect prediction. Yet, even Newtonian systems could behave in ways that seemed unpredictable if tiny differences in starting conditions amplified over time. This sensitivity, later called the “butterfly effect,” became one of chaos theory’s most famous hallmarks. It tells us that in complex systems, a minuscule change—like the flap of a butterfly’s wings—can set off a chain reaction leading to monumental consequences elsewhere. The notion is both terrifying and beautiful: it shows that the universe is intimately connected, with subtle threads linking even the smallest events to grand outcomes.
The Birth of Chaos Theory
Modern chaos theory emerged in the twentieth century, rooted in mathematics and physics. Early pioneers like Henri Poincaré, in the late 1800s, discovered that the motion of three or more celestial bodies—like the Sun, Earth, and Moon—could never be fully predicted. Even deterministic systems, governed by precise laws, could behave unpredictably due to extreme sensitivity to initial conditions. Poincaré’s work revealed that order and chaos are not opposites but exist together in a delicate dance.
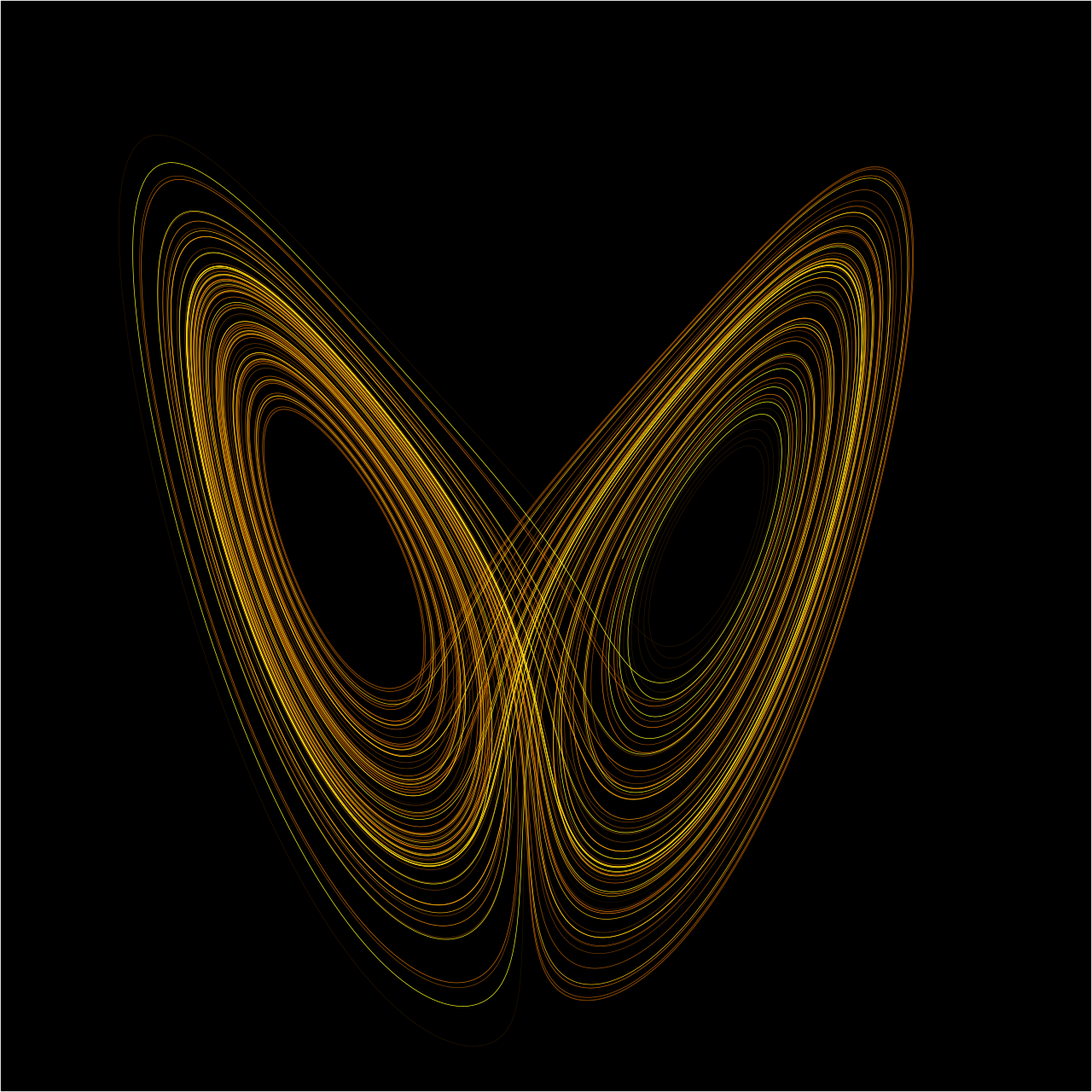
The 1960s brought a revolution. Edward Lorenz, a meteorologist studying weather patterns, stumbled upon a startling discovery while running computer simulations. Small rounding errors in his calculations produced dramatically different outcomes. He realized that weather is not merely complicated—it is chaotic. From this insight arose the iconic image of the butterfly effect and the realization that predictability has limits, even in deterministic systems. Lorenz’s work showed that chaos is not noise or randomness but a new kind of order: deterministic yet unpredictable, structured yet seemingly erratic.
Chaos theory soon expanded beyond meteorology into physics, biology, economics, and social sciences. Scientists began to see the same hidden patterns in systems as diverse as population dynamics, fluid turbulence, cardiac rhythms, and stock markets. The language of chaos—fractals, strange attractors, and bifurcations—became the key to unlocking a universe that is both unpredictable and exquisitely ordered.
Understanding Chaos Through Simple Systems
To grasp chaos, it helps to start with simple examples. Consider a pendulum swinging back and forth. A single pendulum is predictable; its motion repeats in a regular rhythm. Now, imagine two pendulums connected by a spring. The system becomes more complex. Small differences in the starting positions of the pendulums lead to wildly different motions over time. This simple mechanical system exhibits the hallmark of chaos: sensitivity to initial conditions.
Another example comes from population biology. Imagine a species of rabbits reproducing in a forest. If each generation grows at a steady rate, the population may increase predictably. But if growth depends on food availability and environmental pressures, the population can fluctuate chaotically. A small change in initial population numbers can lead to massive variations over generations. Yet, when scientists plot these fluctuations, beautiful patterns emerge. Points cluster around specific shapes called attractors, revealing the hidden order beneath apparent randomness.
These examples illustrate a fundamental principle of chaos theory: complex behavior can arise from simple rules. Unlike random noise, chaotic systems are governed by deterministic laws. They are sensitive, nonlinear, and often fractal in structure. In other words, chaos is not the absence of order but a deeper, more intricate form of organization.
Strange Attractors and Fractals
Central to chaos theory is the concept of attractors. An attractor is a set of states toward which a system tends to evolve. In predictable systems, attractors may be simple points or cycles. In chaotic systems, attractors take on complex, fractal shapes, known as strange attractors. The Lorenz attractor, discovered by Edward Lorenz, is perhaps the most famous example. Its looping, butterfly-shaped structure encapsulates the idea that chaos follows a hidden geometry. Points within the system never settle into a simple pattern but remain confined within the attractor’s boundaries, tracing intricate paths that never repeat exactly.
Fractals are another manifestation of hidden order. These are shapes that repeat at different scales, exhibiting self-similarity. The branching of trees, the structure of rivers, and the jagged outlines of coastlines all display fractal properties. In mathematics, the Mandelbrot set is a quintessential fractal, revealing infinite complexity within simple equations. Fractals show that chaos is not randomness but structured intricacy, where patterns persist across scales. Nature, it seems, thrives on this principle.
Chaos in Nature
Chaos theory illuminates phenomena in nature that once seemed inexplicable. Weather, for example, is famously chaotic. We can predict temperature trends over days, but precise weather patterns remain elusive beyond a short horizon. Atmospheric systems contain countless interacting variables—temperature, pressure, wind, humidity—whose tiny differences amplify over time. Yet within this apparent unpredictability, meteorologists detect patterns: recurring cyclones, jet streams, and seasonal oscillations. Chaos theory explains how nature can be unpredictable and patterned simultaneously.
In biology, chaotic dynamics appear in heart rhythms and brain activity. Healthy heartbeats are not perfectly regular; they exhibit subtle chaotic variations that enable flexibility and resilience. Abnormalities in these patterns can indicate disease. Similarly, neural networks in the brain display chaotic firing patterns, suggesting that cognition, perception, and memory emerge from a delicate balance of order and chaos. Life itself, it seems, thrives at the edge of chaos—a state where systems are neither rigid nor random, but optimally adaptable.
Ecological systems also reflect chaos. Predator-prey relationships, population dynamics, and ecosystem interactions are influenced by nonlinear feedback loops. A small environmental change can cascade through the system, producing dramatic shifts. Chaos theory allows scientists to understand these dynamics, offering insights into conservation, sustainability, and the delicate balance that sustains life on Earth.
Chaos in Human Systems
Beyond nature, chaos theory applies to human society. Economic markets, traffic flow, political systems, and social networks all exhibit chaotic behavior. Stock markets, for instance, are influenced by countless decisions, rumors, and trends. Small perturbations—a single trade, a tweet, a rumor—can propagate through the system, creating volatility. Yet, patterns emerge: cycles, crashes, and trends that reveal underlying structures. Economists and analysts increasingly use chaos theory to model these dynamics, seeking to anticipate instability without assuming simple predictability.
Human behavior itself is partially chaotic. Decisions, emotions, and interactions are influenced by myriad factors that interact nonlinearly. Relationships, for example, can oscillate unpredictably, yet underlying patterns often guide long-term dynamics. In psychology, chaos theory provides a lens to understand complex mental states, creativity, and the emergence of collective behavior. It suggests that unpredictability is not a flaw but an inherent feature of adaptive systems.
The Philosophical Implications of Chaos
Chaos theory challenges our deepest assumptions about the universe. Classical science was built on predictability—the belief that given enough information, the future could be calculated. Chaos reveals the limits of prediction and the subtle interplay of determinism and uncertainty. It suggests that freedom, creativity, and unpredictability are not random anomalies but fundamental aspects of reality.
Philosophically, chaos invites humility. It reminds us that systems are interconnected, that tiny actions can have enormous consequences, and that apparent disorder may conceal profound structure. It blurs the line between science and art, as the fractal beauty of nature emerges from mathematical rules yet appears infinitely creative. Chaos is a language through which the universe expresses complexity, revealing that simplicity and intricacy coexist in every process.
The Edge of Predictability
One of chaos theory’s most striking insights is that predictability has limits. Even in deterministic systems governed by precise laws, tiny uncertainties grow exponentially, limiting our ability to forecast. This is evident in weather, planetary motion, and quantum systems. Yet, even as exact prediction becomes impossible, statistical patterns and structural constraints persist. In other words, we can understand tendencies and probabilities even when specific outcomes remain uncertain.
This notion resonates beyond mathematics. In life, uncertainty is inevitable, yet patterns, habits, and rhythms guide our choices. Chaos theory mirrors this truth: the universe is not wholly arbitrary, but it is never fully predictable. Order and disorder are intertwined, producing the dynamic richness of reality.
Chaos as a Creative Force
Chaos is not merely destructive or disorienting; it is a source of creativity and adaptation. In ecosystems, fluctuating populations allow evolution to explore new niches. In the brain, chaotic neural patterns enable flexible thinking, problem-solving, and artistic innovation. In human societies, unpredictability drives cultural evolution, economic experimentation, and scientific discovery. Chaos is not the enemy of order but its complement, sustaining diversity, resilience, and novelty.
Artists, musicians, and writers have long recognized chaos’s aesthetic dimension. The fractal patterns of clouds, the turbulent flow of rivers, and the branching of lightning inspire awe. By understanding the hidden order within chaos, we gain a deeper appreciation of beauty and complexity in both nature and human creation.
The Mathematical Heart of Chaos
At its core, chaos theory relies on nonlinear mathematics. Linear systems, like a simple pendulum, behave predictably; outputs are proportional to inputs. Nonlinear systems, however, respond in complex ways: small inputs can lead to large effects, interactions produce feedback loops, and trajectories diverge over time. Mathematicians use differential equations, iterative maps, and fractal geometry to model these systems. These tools reveal that what appears random is often deterministic, shaped by precise—but sensitive—rules.
Strange attractors, bifurcation diagrams, and fractal structures provide windows into chaotic dynamics. They show that even simple equations can generate infinitely complex behaviors. This mathematical insight bridges theory and observation, explaining turbulence in fluids, oscillations in populations, and fluctuations in markets. Chaos theory thus provides both conceptual clarity and predictive power, despite inherent limitations.
The Universal Presence of Chaos
Chaos is not confined to mathematics or science; it is a universal principle. From galaxies spiraling in space to the delicate folding of proteins in cells, from the rhythm of the heartbeat to the volatility of human emotions, chaos shapes reality. Recognizing this hidden order transforms our perception of the world. We see not randomness but a subtle choreography, a dance between determinism and unpredictability, simplicity and complexity.
The universe, in its chaotic elegance, invites wonder. It reminds us that uncertainty is not a flaw to be eliminated but a fundamental aspect of existence. It challenges our desire for control, urging us to embrace curiosity, resilience, and creative adaptation. Chaos is not merely a scientific concept; it is a lens through which we can understand life itself.
Conclusion: Embracing the Hidden Order
Chaos theory teaches us that the universe is simultaneously unpredictable and structured, random and patterned, turbulent and beautiful. It reveals the profound interplay between simplicity and complexity, determinism and uncertainty. Through strange attractors, fractals, and nonlinear dynamics, we glimpse the hidden order that governs seemingly chaotic systems.
In everyday life, chaos is everywhere—traffic flows, weather patterns, social interactions, and personal choices. Yet, by understanding the underlying principles, we can navigate uncertainty with insight and grace. Chaos is not merely disorder; it is a creative force, a source of beauty, and a fundamental truth of the cosmos.
By studying chaos, we learn to appreciate the subtle patterns that shape our world. We discover that unpredictability is not a limitation but a dimension of possibility. The universe, in its intricate dance of chaos, invites us to observe, wonder, and participate in the unfolding mystery. In embracing chaos, we embrace life itself—the hidden order within apparent disorder, the infinite complexity within simplicity, and the profound beauty that arises when unpredictability meets structure.
The hidden order inside chaos is not only a scientific discovery; it is a philosophical revelation. It reminds us that even in uncertainty, patterns exist; even in disorder, structure emerges; and even in the wildest turbulence, beauty persists. Chaos theory offers not only understanding but inspiration: a vision of a universe where unpredictability and order coexist in eternal, harmonious dance.