In the fascinating world of quantum physics, reality often defies common intuition. Concepts such as superposition, entanglement, and quantum tunneling challenge our everyday understanding of the universe. Yet, tucked away within this already perplexing landscape lies an even deeper mathematical elegance: duality. Duality in quantum physics refers to profound transformations that relate seemingly distinct physical theories—bridges across different worlds of description that, remarkably, describe the same phenomena.
Now, a team of physicists from the University of Cambridge, Ghent University, the Institut des Hautes Études Scientifiques (IHÉS), and the University of Sydney have moved this abstract idea from the realm of pure theory into something tangible. In a study recently published in Physical Review Letters, they have demonstrated that these elusive dualities can be implemented as quantum circuits, constructed with real quantum gates and operating within a unitary framework.
This groundbreaking work doesn’t just refine our understanding of duality—it unlocks practical tools for exploring the deepest structures of quantum systems, with implications for quantum computation, materials science, and the fabric of spacetime itself.
Rethinking Symmetry in Quantum Worlds
At its core, symmetry in physics is a statement about invariance—how a system remains unchanged under certain transformations. Classical physics is rife with symmetries: rotating a sphere or sliding a frictionless puck along a surface both leave the system unchanged. In quantum mechanics, however, symmetry becomes more nuanced. Here, it’s not just about maintaining appearances—symmetry affects the very nature of interactions, correlations, and the types of states that a quantum system can occupy.
In traditional lattice models, used to study quantum many-body systems, symmetries are typically implemented “on-site,” meaning each site in the lattice transforms independently. But in recent years, researchers have discovered that this is an artificial limitation. More general forms of symmetry can create entanglement across neighboring sites, weaving quantum correlations directly into the fabric of space itself.
These types of symmetries are more naturally described not as simple operators, but as matrix product operators—a powerful class of tensor networks that explicitly encode complex, non-local entanglement structures. This insight forms the backbone of the new research: if symmetries can be entangled and distributed, so too can dualities.
Fusion Categories: The Mathematics Behind Duality
To turn dualities into operational tools, the researchers had to delve deep into the mathematical machinery of fusion categories. These are abstract algebraic structures that underpin many of the strange phenomena in quantum field theory, topological phases of matter, and string theory. Fusion categories describe how objects (such as particle-like excitations or symmetry sectors) combine and interact—essentially a quantum version of multiplication tables.
By using the representation theories of these categories, the researchers were able to systematically construct symmetry operators as matrix product operators. They realized that duality transformations, long thought to be non-invertible and thus non-unitary, could also be framed in this language.
This was a major leap. If dualities could be encoded as matrix product operators, perhaps they could also be implemented physically—as quantum circuits—on real quantum computers. But first, the team had to resolve a fundamental paradox.
The Puzzle of Non-Invertibility
Traditionally, dualities have been viewed as irreversible. When applied to a quantum system, a duality transformation might produce a new representation of the system—one where operators and degrees of freedom are radically redefined. In many cases, some information is “lost,” or at least inaccessible, during this process. Physicists call these transformations non-invertible symmetries.
This non-invertibility implies non-unitarity—a fatal flaw when attempting to build a quantum circuit, which by definition must be unitary (i.e., it must preserve total quantum information).
However, Laurens Lootens and his colleagues discovered a crucial loophole. What if, instead of treating the boundary conditions of a system as fixed, they were incorporated into the quantum degrees of freedom? By allowing the duality transformation to act on the boundary conditions—not just the bulk of the system—they found that no information was lost. The transformation could be reversed. The duality became, astonishingly, unitary.
In technical terms, this meant enlarging the Hilbert space of the system—adding ancillary degrees of freedom to track sector information. With this enlarged viewpoint, the transformation ceased to be paradoxical. It became circuit-realizable.
Building the Circuit: Linear Depth and Optimal Design
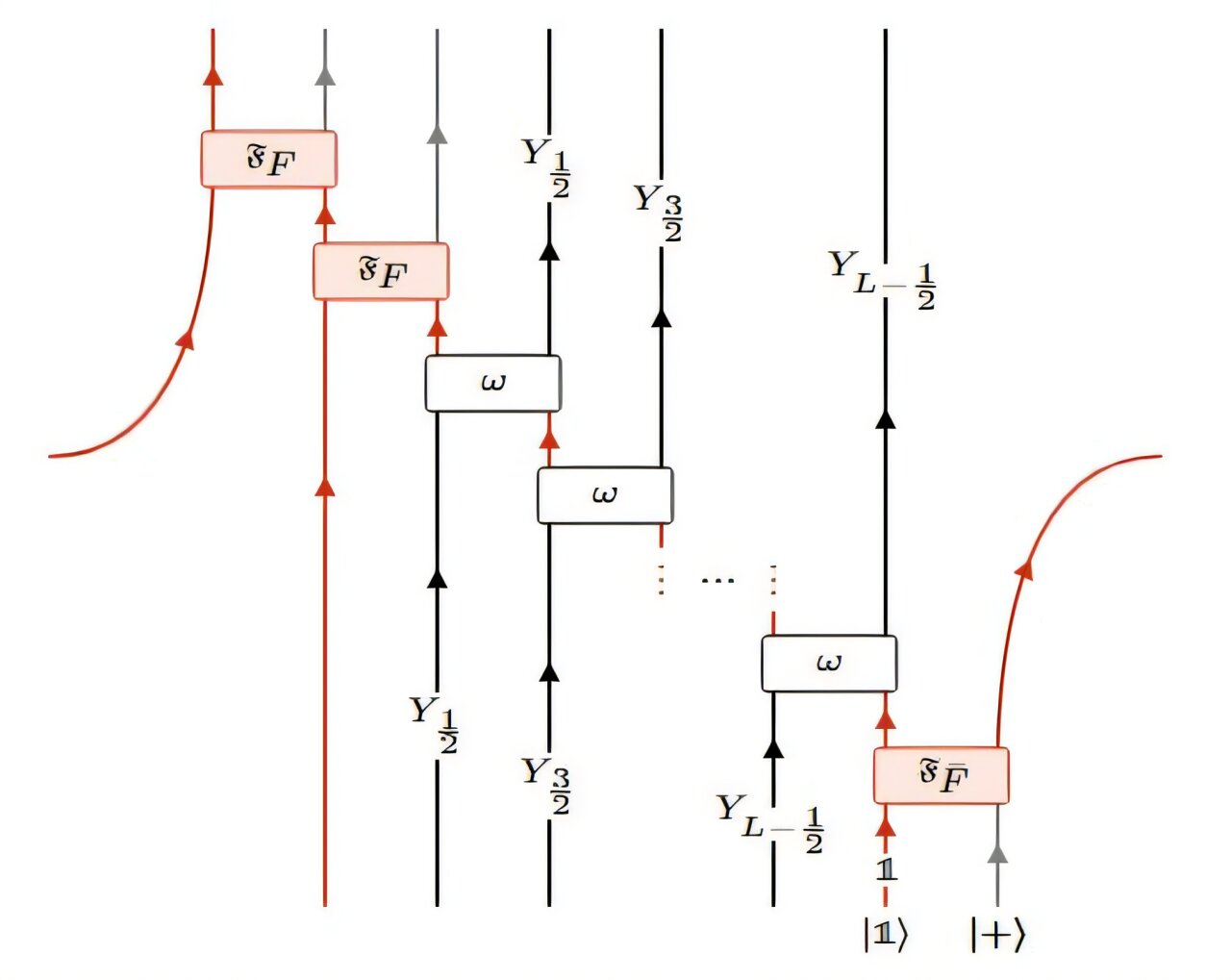
Armed with this new understanding, the team translated these duality operators into quantum circuits—sequences of quantum gates that could be implemented on hardware. The circuit depth—defined as the number of time steps (layers) needed to complete the operation—turned out to be linear with respect to the size of the system.
That might sound like a computational hurdle, but in this context, it was actually a sign of optimality. Since dualities can convert local operators into non-local string operators, any faithful implementation must reflect this non-locality. A depth equal to system size means each part of the system is sequentially linked—a physical manifestation of the duality’s logic.
Clement Delcamp, co-author of the paper, elaborated: “The dualities we consider essentially amount to generalized gauging procedures. These are typically non-invertible in closed boundary conditions, and a fortiori non-unitary. But using our previous results, we showed that if you supplement the Hilbert space with ancillary degrees of freedom and then perform a measurement, you can project the system into definite sectors and restore unitarity.”
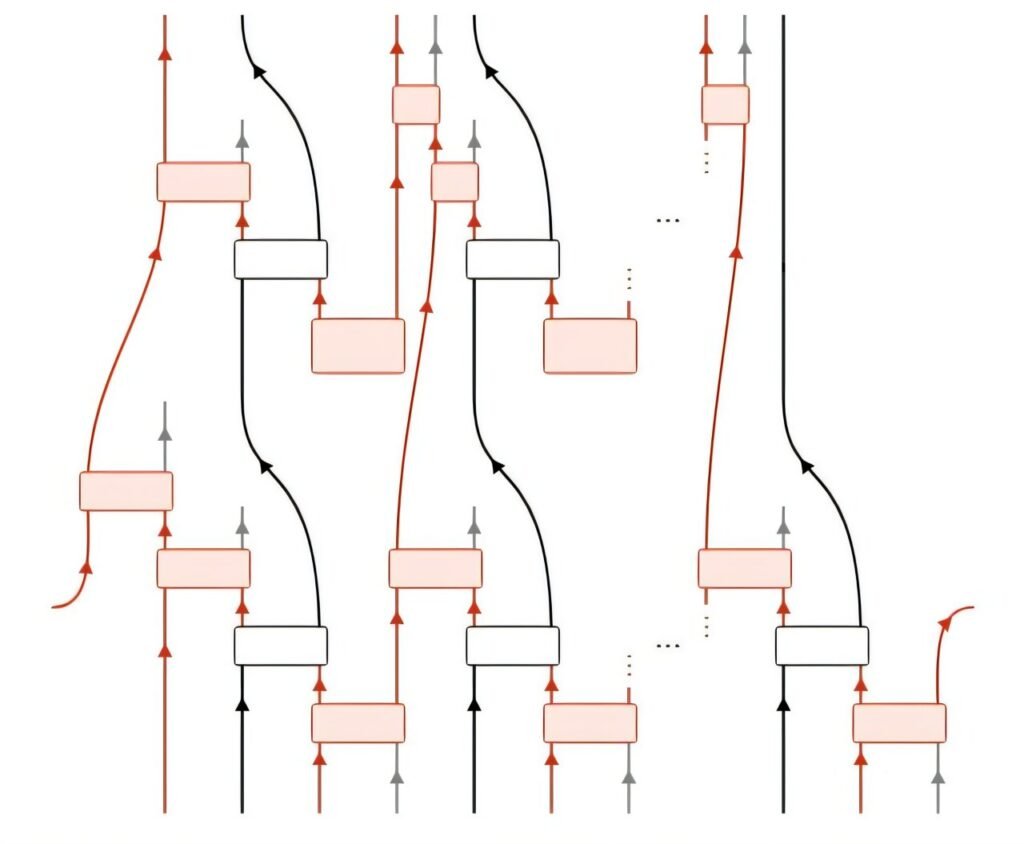
This insight reframes the nature of non-unitarity in quantum systems. It’s not a limitation, but a signpost—pointing to hidden structure, to extra dimensions of information encoded in the boundaries of the system.
Quantum Channels and Information Flow
Another fascinating consequence of this work is the reinterpretation of dualities as quantum channels. In general, a quantum channel describes the flow of information in an open system, often involving measurement, noise, or interaction with an environment. When dualities are applied and ancillary systems are measured, the resulting operation fits the definition of a quantum channel: not quite a reversible evolution, but a structured transformation of quantum states.
This insight links dualities to quantum error correction, entanglement distillation, and even quantum gravity, where the language of channels and sectors plays an increasingly prominent role. The notion that non-unitary transformations can be embedded within unitary circuits through smart bookkeeping of sector data opens up powerful avenues for modular quantum algorithms, where complex symmetry operations are broken down into controllable subroutines.
Generalizing to All (1+1)D Quantum Models
One of the most striking aspects of the team’s achievement is its generality. This isn’t just a trick that works for one model, or one class of dualities. The researchers showed that their framework applies to arbitrary dualities between arbitrary (1+1)-dimensional quantum lattice models with arbitrary internal symmetries. That level of generality is rare in quantum physics, where even minor changes in assumptions can lead to wildly different behavior.
This universality makes the work immediately relevant across a wide swath of theoretical physics. Whether one is studying spin chains, topological phases, symmetry-protected edge states, or even low-dimensional analogs of quantum gravity, the ability to realize dualities as linear-depth unitary circuits opens up a new toolkit.
Toward Higher Dimensions and Topological Realms
Of course, the next challenge looms large: generalizing these insights to higher dimensions. In more than one spatial dimension, the mathematical tools become more complex. The researchers hint that they will need to engage with higher category theory, a cutting-edge mathematical framework that extends beyond traditional group theory to capture richer interrelations among symmetries and excitations.
While daunting, the rewards of such a generalization are immense. Many of the most exotic phases of matter—those with anyons, topological orders, and quantum error-correcting properties—live in higher dimensions. If dualities in these systems can be turned into circuits, the path to topological quantum computation becomes clearer.
Encouragingly, there are already successful examples of quantum circuits being used to prepare exotic states of matter on real quantum hardware. This suggests that the theoretical results are not just abstract—they are practically realizable, perhaps even within the next generation of quantum processors.
The Road Ahead: Mapping the Duality Landscape
As the researchers continue their work, several intriguing questions remain. One particularly important open problem is understanding which types of dualities can be implemented with constant-depth circuits—those that require only a fixed number of steps regardless of system size. The team has identified a class of “nilpotent” dualities where this is possible, but the full classification remains elusive.
The practical upshot is that if constant-depth implementations can be characterized fully, they may unlock highly efficient quantum algorithms for manipulating symmetry sectors, generating entangled states, and probing topological phenomena.
In a broader sense, the success of this work underscores a deep philosophical point about physics and computation: that the symmetries and structures of nature, no matter how abstract or exotic, are not beyond reach. They can be built, enacted, and explored—not just in the mind, but in the laboratory.
Final Reflections: A Bridge Between Theory and Device
What the team from Cambridge, Ghent, IHÉS, and Sydney has done is nothing short of alchemy. They have taken one of the most subtle and profound ideas in theoretical physics—duality—and shown how to realize it on a quantum machine. Their method opens a portal between the abstract mathematical realms of fusion categories and tensor networks and the concrete, device-oriented world of quantum circuits and gate sequences.
In doing so, they have created not only a new toolset for physicists and engineers, but a new vision: one where the hidden symmetries of the universe don’t just guide our theories, but power our machines.
Quantum duality, once the province of blackboards and thought experiments, is now a blueprint—etched in code, ready to run.
Reference: Laurens Lootens et al, Low-Depth Unitary Quantum Circuits for Dualities in One-Dimensional Quantum Lattice Models, Physical Review Letters (2025). DOI: 10.1103/PhysRevLett.134.130403