In a world that often feels unpredictable—where weather changes abruptly, stock markets crash without warning, and a butterfly flapping its wings in Brazil might be blamed for a tornado in Texas—humans crave order. We seek patterns in clouds, rhythms in data, and meaning in coincidence. But there exists a branch of science that challenges our assumptions about predictability and order. It’s called chaos theory, and at its heart lies a paradox: even in systems that appear random, there can be profound, underlying structure.
Chaos theory is not about complete disorder. It’s about systems so sensitive to initial conditions that they behave unpredictably in practice, even though they are governed by deterministic laws. It is a field that has reshaped our understanding of everything from planetary motion to heart rhythms, from the spread of diseases to the flight of a hummingbird. To understand chaos theory is to appreciate how the universe can be simultaneously orderly and unpredictable, a cosmic dance between determinism and surprise.
A Glimpse into the Birth of Chaos
For centuries, scientists and mathematicians embraced the Newtonian worldview—a universe governed by fixed laws, where the future could be predicted with precision if one knew the present perfectly. In this paradigm, the universe was a giant clock, and with the right equations, everything could be forecast.
But cracks in this deterministic vision began to show in the 19th century. One of the earliest hints came from the work of Henri Poincaré, a French mathematician. While studying the three-body problem—predicting the motion of three gravitationally interacting celestial bodies—Poincaré realized something astounding. Despite following strict laws of motion, the behavior of such a system could become wildly unpredictable. Tiny changes in initial conditions could result in drastically different outcomes. This was a radical departure from the tidy world of Newton.
Yet, the true birth of chaos theory as a recognized scientific field didn’t occur until the 1960s, thanks to meteorologist Edward Lorenz. Lorenz was running computer simulations of weather patterns when he noticed something peculiar: when he rounded one of the input numbers ever so slightly, the resulting simulation diverged dramatically from the original. This was not due to machine error, but due to the system’s extreme sensitivity to initial conditions—a hallmark of chaos. The so-called “butterfly effect” was born, and chaos theory began to take root in mainstream science.
The Butterfly Effect: Tiny Causes, Massive Effects
The butterfly effect is one of the most poetic and often misunderstood concepts in chaos theory. Its name derives from the metaphor that a butterfly flapping its wings in South America could influence the formation of a hurricane weeks later in North America. While not to be taken literally, the metaphor captures the essence of chaos: in certain systems, tiny inputs can lead to dramatically different outcomes.
What makes these systems chaotic is not randomness but deterministic unpredictability. That is, the rules are clear and fixed, but their results defy long-term prediction. Imagine dropping two balls from nearly identical heights into a pinball machine filled with bumpers. For a while, their paths will look similar, but soon they will diverge radically, bouncing in directions that seem uncorrelated. The laws of physics still govern every bounce, but the tiny initial difference grows exponentially over time.
This sensitivity makes long-term forecasting practically impossible for chaotic systems. It’s why weather predictions beyond a week become unreliable and why even the most sophisticated financial models can’t fully predict market behavior. Yet, there is a strange beauty in this unpredictability—a hidden order that gives rise to intricate patterns.
Strange Attractors and Fractals: Geometry in Motion
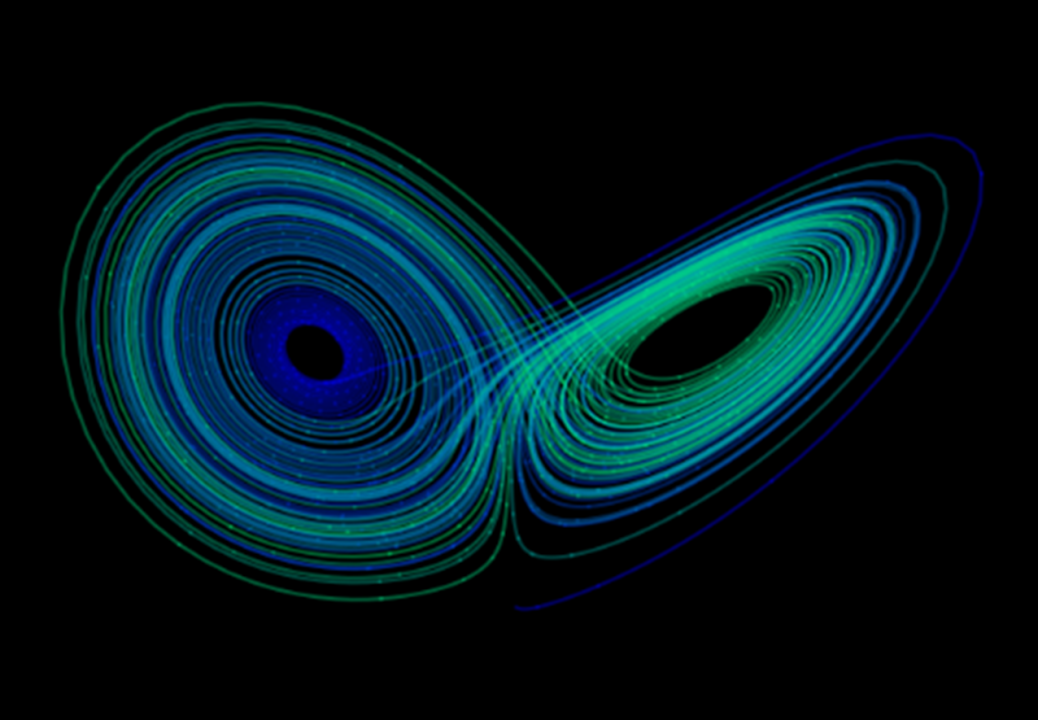
As scientists delved deeper into chaotic systems, they discovered that these seemingly erratic behaviors were not random after all. They often gravitated toward specific geometric patterns known as strange attractors. These are shapes in the system’s phase space—the multidimensional space in which all possible states of a system are represented—that the system’s trajectory follows.
The Lorenz attractor is one of the most famous examples. It resembles a butterfly or a pair of wings and represents how a simplified weather model evolves over time. Even though the system never repeats exactly, it remains bounded within a particular shape. The attractor reveals that chaos has structure, a skeleton of form hidden beneath the flux.
Closely related to attractors are fractals, geometric figures characterized by self-similarity and infinite complexity. Fractals appear not only in abstract mathematics but throughout nature—in coastlines, clouds, mountain ranges, blood vessels, and even broccoli. Benoît Mandelbrot, a pioneer in fractal geometry, famously said, “Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth.”
Fractals provide a language to describe the geometry of chaos. They help us visualize how complexity arises from simplicity and how natural forms evolve under iterative, recursive processes. In essence, fractals are the fingerprints of chaotic systems.
Chaos in Nature: The Wild Rhythms of Reality
The reach of chaos theory extends far beyond weather and mathematics. It shows up in biology, chemistry, physics, economics, and beyond. In nature, chaos is not the exception—it is often the rule.
Consider the human heart. While a healthy heartbeat may seem regular, its rhythm is actually subtly irregular—a sign of health and adaptability. A perfectly regular beat, on the other hand, can be a precursor to cardiac arrest. Researchers have discovered that the heart’s rhythm is governed by nonlinear dynamics, and sudden arrhythmias can arise from chaotic transitions within the cardiac system.
In ecology, predator-prey relationships can also demonstrate chaotic behavior. A slight change in the number of prey can lead to significant changes in the predator population, which in turn affects the prey in unpredictable ways. These dynamics make managing ecosystems a delicate and often counterintuitive task.
Even in the brain, chaotic patterns are at play. Neural activity, while not entirely random, exhibits complex fluctuations that defy simple patterns. Some theories suggest that the brain uses chaotic dynamics to allow for flexibility, creativity, and responsiveness to changing environments. Seizures, by contrast, may represent a breakdown of this complex order into simpler, pathological rhythms.
From the flapping of bird wings to the swirl of a hurricane, chaos is the engine behind nature’s variability and creativity.
Chaos in Human Systems: Markets, Minds, and Movements
Human-created systems, too, are not immune to chaos. Financial markets, for instance, are prime examples of chaotic behavior. While traders and analysts attempt to forecast market trends, tiny changes in sentiment, regulation, or information can cause massive ripples. These markets are driven by nonlinear interactions among millions of participants, each with their own psychology, objectives, and imperfections.
Political and social movements often display chaotic dynamics. Revolutions, protests, and ideological shifts can emerge from small events—a tweet, a protest, an arrest—and rapidly cascade into sweeping transformations. The Arab Spring, for instance, was catalyzed by a single incident in Tunisia but quickly spiraled into regional upheaval.
In psychology, chaos theory has found a foothold in understanding human cognition and behavior. Our thoughts, emotions, and actions often follow nonlinear paths. A minor comment can spark a major emotional response. A chance encounter can redirect a life. Chaos theory offers a framework for understanding the unpredictability of human development and the complex interplay of memory, experience, and identity.
Even language and art bear traces of chaos. Poets and painters often rely on spontaneous inspiration, and meaning emerges through iteration and experimentation rather than through linear planning. Creativity itself might be one of the most chaotic of all human processes—a dance between structure and improvisation.
Determinism vs. Free Will: The Philosophical Ripple
The implications of chaos theory extend beyond science into philosophy. If deterministic systems can behave unpredictably, what does this say about free will and fate? Classical determinism held that the universe’s future was fixed, given its present state and the laws of physics. Chaos theory complicates this view by showing that even deterministic systems can evolve in ways that are, in practice, impossible to predict.
This introduces a nuanced view of human freedom. While our actions may be governed by laws of biology, chemistry, and physics, the sensitivity and complexity of these systems might leave room for genuine spontaneity. Chaos doesn’t guarantee free will, but it suggests that the future is not strictly preordained. It opens the door to emergence, to novelty, and perhaps to choice.
In this sense, chaos theory becomes not only a scientific concept but a philosophical lens—a way to reconcile structure and freedom, rules and randomness.
Chaos and the Limits of Knowledge
One of the humbling lessons of chaos theory is that it reveals the limits of human knowledge. No matter how powerful our computers or sophisticated our models, we cannot predict the weather months in advance, the markets a year ahead, or the precise path of a double pendulum after enough time has passed.
This is not due to a lack of information or intelligence but to the nature of complex systems themselves. Initial conditions can never be known with absolute precision, and small errors will inevitably amplify. In a chaotic system, uncertainty is not a bug; it is a feature.
But this limitation is not a failure. It reminds us to approach science—and life—with humility. It encourages us to focus not just on prediction but on understanding, adaptation, and resilience. It teaches us to navigate complexity with flexible strategies rather than rigid plans.
The Beauty of Chaos: From Equations to Art
For many scientists and artists alike, chaos is not merely a subject of study—it is a source of inspiration. The equations that produce chaotic behavior often generate stunning visual forms. The Mandelbrot set, perhaps the most famous fractal, contains infinite layers of beauty within its boundaries. Zooming into its curves reveals ever more intricate structures, a mathematical hall of mirrors.
Music, too, can embrace chaos. Composers have experimented with fractal patterns, irregular rhythms, and nonlinear structures to create pieces that feel organic and surprising. Painters like Jackson Pollock used chaotic motion in their technique, creating works that resonate with the dynamism of nature.
There is an aesthetic dimension to chaos that mirrors its scientific significance. Just as a storm cloud or lightning bolt evokes awe through its unpredictable grace, so too does chaos challenge our minds and stir our imagination.
Conclusion: Embracing the Unpredictable
Chaos theory teaches us to see the world with new eyes. It reminds us that unpredictability does not imply disorder and that complexity can arise from the simplest rules. It reveals the deep, hidden structures that shape our lives, even as they defy our control.
In an age obsessed with certainty and control, chaos offers a more nuanced vision. It invites us to dance with unpredictability rather than fight it, to adapt rather than dominate, to marvel rather than despair. Whether in the patterns of the clouds, the beating of a heart, or the unfolding of a life, chaos is ever-present—not as a force of destruction, but as a wellspring of creativity and change.
In chaos, we find not the end of understanding but its true beginning.