Everywhere we look, the universe is spinning. Galaxies whirl through the vastness of space, stars rotate on their axes, and planets orbit suns in an endless cosmic ballet. But this isn’t just a poetic metaphor; it’s a fundamental truth of physics. At the heart of this swirling cosmic dance lies one of the most important and fascinating principles in all of physics: angular momentum.
Angular momentum is the quantity that governs all rotational motion. It is why figure skaters spin faster when they pull in their arms, why Earth continues to rotate day after day, and why stars collapse into rapidly rotating neutron stars when they die. It appears in systems as small as atoms and as vast as galaxies, a quiet yet powerful law that maintains the rhythm of motion in a universe that never truly stands still.
Understanding angular momentum is to peer into the mechanics of spinning worlds, to glimpse the hidden symmetry that keeps planets orbiting and galaxies alive. It’s not only central to classical physics but also crucial in quantum mechanics, where even particles too small to see exhibit rotational properties. This article will take you on a journey into the heart of angular momentum, from its earliest conceptual roots to its farthest-reaching implications in the cosmos.
Foundations: Linear Momentum and Rotation
Before diving into angular momentum, we need to revisit its close relative: linear momentum. In simple terms, linear momentum is the quantity of motion an object has while moving in a straight line. It is the product of an object’s mass and velocity. The heavier and faster an object is, the more momentum it possesses.
Linear momentum helps us understand collisions, explosions, and the motion of objects under forces. However, much of the motion we observe in the universe is not linear, but rotational. Wheels turn, planets spin, and even electrons whirl about their atomic nuclei. To describe this type of motion, physicists needed something more — a rotational equivalent to linear momentum. That concept is angular momentum.
Angular momentum can be thought of as the “rotational inertia” of an object in motion. It’s not just about how fast something is spinning, but also how far its mass is from the axis of rotation. It is this combination — of rotational speed and distribution of mass — that defines how difficult it is to change an object’s spin.
What Exactly Is Angular Momentum?
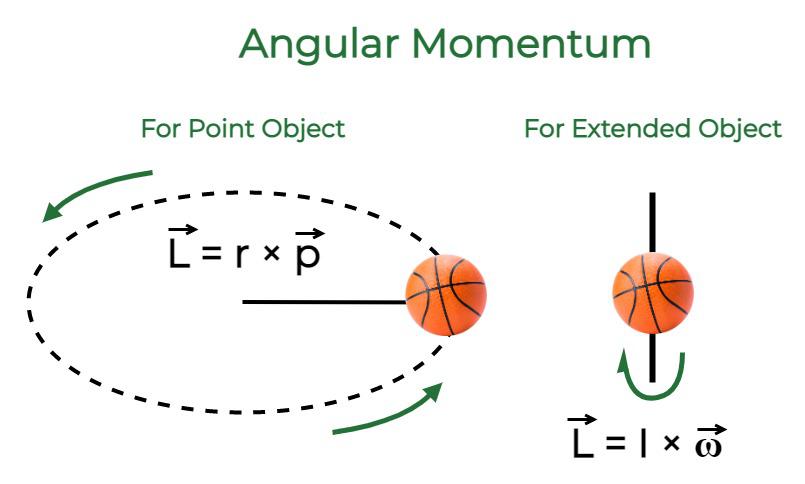
Angular momentum, symbolized by the letter L, is a vector quantity. That means it has both magnitude (how much) and direction (which way). It’s calculated differently depending on whether you’re looking at a single rotating object or an extended system, but the core idea is the same: it is the rotational analog of linear momentum.
For a single particle moving in a circle, angular momentum is the cross product of its position vector and its linear momentum vector. In mathematical terms:
L = r × p
Here, r is the position vector (the distance from the axis of rotation to the particle), and p is the linear momentum (mass times velocity). The cross product means that angular momentum is perpendicular to the plane of rotation, aligning with the axis around which the motion occurs.
For rigid bodies like spinning disks or planets, the formula simplifies:
L = Iω
Here, I is the moment of inertia — a measure of how mass is distributed relative to the axis — and ω (omega) is the angular velocity, or how fast the object is spinning.
This deceptively simple equation hides deep truths about how systems behave. As with linear momentum, angular momentum is conserved. That means if no external torque acts on a system, its total angular momentum remains constant. This is the key to understanding everything from the graceful pirouette of a ballerina to the fiery collapse of a dying star.
Conservation: The Sacred Rule of Rotation
The conservation of angular momentum is one of the most powerful principles in physics. In a closed system, where no external torques interfere, the total angular momentum stays the same. This law is not a mere mathematical curiosity; it is a physical truth that governs the behavior of rotating bodies across the cosmos.
One of the most familiar examples of angular momentum conservation can be seen in figure skating. When a skater pulls in their arms during a spin, their moment of inertia decreases. Since angular momentum must be conserved, their angular velocity increases — they spin faster. When they extend their arms again, the moment of inertia increases, and the spin slows down.
This same principle is at play in the cosmos. When a massive star runs out of nuclear fuel, it can collapse under its own gravity, forming a dense neutron star. As its radius shrinks dramatically, its moment of inertia decreases. To conserve angular momentum, it begins spinning incredibly fast — some neutron stars spin hundreds of times per second.
It’s the same reason why planets continue orbiting stars without slowing down, and why galaxies can maintain their spin across billions of years. In the vacuum of space, with few external torques to interfere, angular momentum reigns supreme.
Torque: The Force That Changes Spin
While angular momentum is conserved in a closed system, it can be changed when external influences come into play. The rotational equivalent of force is torque, and it is torque that changes angular momentum.
Just as force causes a change in linear momentum, torque causes a change in angular momentum. Torque is generated when a force is applied at a distance from an axis of rotation. The greater the force or the farther from the axis it is applied, the greater the torque.
You experience torque every time you open a door. If you push near the hinge, the door resists. Push at the edge, and it swings easily. That’s torque in action.
In the cosmos, torque is responsible for many fascinating behaviors. Gravitational interactions between celestial bodies exert torques that can change their rotational speeds or axes. The tidal forces between the Earth and Moon, for instance, have gradually slowed Earth’s rotation and caused the Moon to become tidally locked — it shows the same face to us as it orbits.
Without torque, angular momentum remains constant. With it, worlds can be tilted, spins can be reversed, and orbits can shift over time.
The Quantum Realm: Angular Momentum Goes Subatomic
As we descend from the scale of spinning galaxies to the microscopic world of particles, angular momentum does not disappear — it becomes even more intriguing. In quantum mechanics, angular momentum is not just a matter of rotating objects but a fundamental property of particles themselves.
Quantum angular momentum comes in two flavors: orbital and spin. Orbital angular momentum describes how particles like electrons “orbit” the nucleus, not in classical paths, but in probabilistic clouds. Spin, on the other hand, is an intrinsic form of angular momentum. Electrons, protons, and other particles possess spin even though they are point-like and have no physical surface to rotate.
This quantum spin gives rise to magnetic properties. For example, the spin of electrons is what underlies magnetism in materials like iron. When the spins of many electrons align, their tiny magnetic fields combine to create a noticeable magnetic force.
Spin is also subject to quantum rules: it can only take certain discrete values. For electrons, protons, and neutrons, the spin is ±½, meaning they are fermions. Other particles like photons have integer spins and are called bosons. This distinction underlies the structure of matter and the behavior of forces at the most fundamental level.
In particle accelerators, quantum angular momentum governs how particles scatter and interact. It’s a guiding principle in the construction of atomic models and helps explain the stability of atoms, the periodic table, and the behavior of light.
Spinning Planets, Moons, and Stars
Back in the realm of astrophysics, angular momentum governs the structure and evolution of celestial bodies. Planets form from rotating disks of gas and dust around young stars. As material collapses under gravity, it spins faster, and angular momentum dictates the structure of the resulting planet or star.
This is how the solar system acquired its general pattern of rotation. Most planets orbit in the same direction because they inherited their angular momentum from the original rotating disk of the Sun’s formation. The same is true for moons around planets and rings around gas giants.
Angular momentum also explains why planets are not perfect spheres. As they spin, centrifugal force causes them to bulge at the equator. The faster a planet spins, the more pronounced this equatorial bulge becomes. Saturn, with its rapid rotation, is noticeably flattened.
Stars are also subject to the effects of angular momentum. As they evolve and collapse, their rotational speeds increase. This process can result in spinning white dwarfs, neutron stars, and even black holes, all possessing enormous angular momentum.
Galaxies and Cosmic Rotation
Zooming out to the scale of galaxies, angular momentum continues to shape the cosmos. Galaxies rotate — not as solid bodies, but with stars orbiting the center in vast spirals. This rotation influences their structure and helps maintain the beautiful spiral arms seen in galaxies like our Milky Way.
How galaxies acquire their spin is still an area of active research, but it is thought to originate from tiny variations in the early universe. As matter clumped together under gravity, small torques from neighboring regions caused galaxies to begin spinning.
Angular momentum is also crucial in the formation of accretion disks — structures of rotating matter around black holes, neutron stars, and young stars. These disks can be incredibly hot and dense, giving off intense radiation and playing a role in star formation and the growth of massive black holes.
Even clusters of galaxies have angular momentum. The universe is not static, and its structures are not randomly oriented. There is a flow, a spin, a hidden choreography that stretches across billions of light-years, all influenced by the conservation of angular momentum.
Human Mastery: Angular Momentum on Earth
Angular momentum isn’t just a cosmic principle — it plays a vital role in technology, sports, and engineering on Earth. From spinning satellites to balance bikes, humans have learned to harness this principle in countless ways.
Gyroscopes, for example, use the conservation of angular momentum to maintain orientation. They are critical in aircraft, spacecraft, and smartphones. When a gyroscope spins, its axis resists changes in direction, making it a perfect tool for navigation.
In sports, angular momentum explains the spins and flips of gymnasts, the curve of a soccer ball, and the stability of a bicycle. Understanding how to manage spin allows athletes to achieve greater control, speed, and accuracy.
Even in video games and animation, angular momentum is modeled to create realistic movement. It is one of the many hidden forces that makes simulated worlds feel believable.
The Future of Angular Momentum: Research and Beyond
Angular momentum continues to be a fertile ground for discovery. In quantum computing, spin states of particles are used as qubits — the building blocks of a new kind of computer. In astrophysics, gravitational wave detectors like LIGO measure the angular momentum of colliding black holes, revealing secrets of the universe.
New theories in physics often touch on angular momentum. In string theory and quantum gravity, spin and rotation are woven into the fabric of spacetime itself. Angular momentum may hold keys to unifying the laws of physics, from the quantum scale to the cosmic.
As humanity explores new frontiers — colonizing Mars, building space stations, and sending probes beyond the solar system — understanding and mastering angular momentum will remain essential. Whether docking spacecraft or navigating interstellar travel, the laws of rotation will guide us.
Conclusion: The Eternal Spin of Existence
Angular momentum is more than a formula — it is a principle that echoes through every corner of the universe. From the graceful motion of a spinning top to the spiraling arms of galaxies, from the quantum spin of particles to the orbit of planets, it is the rhythm of motion itself.
To study angular momentum is to see the universe in motion and to understand why it does not fall into stillness. It is a window into the balance, symmetry, and continuity that make our cosmos not just dynamic but comprehensible.
As we watch the stars twirl above or a child spin in joy on a playground, we are seeing the same fundamental law at work — a quiet, unwavering conservation that underlies the drama of existence. Angular momentum is not just a concept of physics; it is the signature of motion, the music of the cosmos, and a reminder that nothing in the universe stands still.