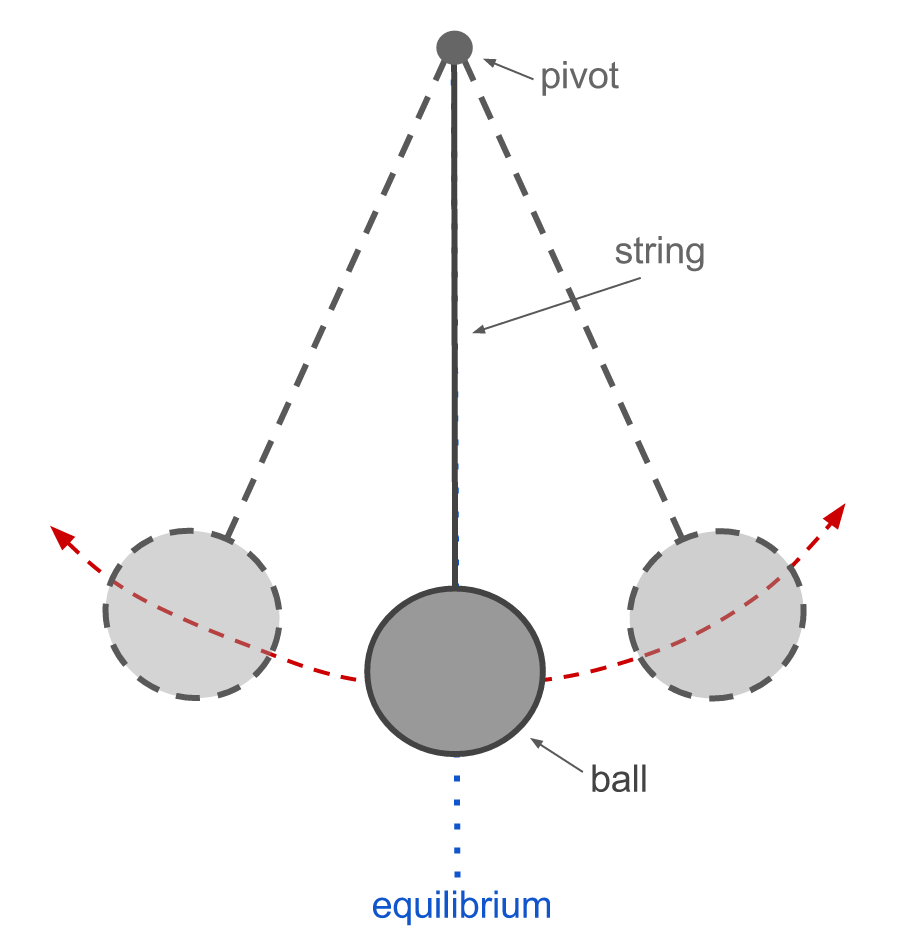
Few images in the history of science are as iconic as that of a swinging pendulum. Whether it’s a grandfather clock rhythmically ticking through the centuries or Foucault’s giant pendulum tracing the Earth’s rotation in a quiet museum hall, this simple device captivates the imagination. At first glance, it seems like nothing more than a weight swinging back and forth, but delve into the physics, and a universe of intricacies opens up. From the early experiments of Galileo Galilei to the high-precision pendulums of modern metrology, the pendulum is more than a device—it is a key that unlocked the secrets of motion, time, and the forces that bind the cosmos.
Galileo’s First Observations
The tale of the pendulum’s significance begins in the 17th century, with a young Galileo observing a chandelier sway in a cathedral in Pisa. The story goes that he noticed, despite the amplitude of the swing changing, the time it took for each oscillation remained the same. Fascinated, he began to time the swings using his own pulse. This simple observation led to the discovery of a phenomenon known as isochronism—the principle that the period of a pendulum remains constant regardless of its amplitude, at least for small angles.
This observation defied the expectations of the time and planted the seeds for a new understanding of motion. Galileo had stumbled upon a system whose behavior was predictable and repetitive. In an age when timekeeping was inconsistent and cumbersome, this was nothing short of revolutionary.
Anatomy of a Pendulum
At its core, a pendulum consists of a mass (called a bob) suspended from a fixed point by a string or rod. When the bob is displaced from its equilibrium position and released, gravity acts to return it to the lowest point, causing it to accelerate. However, due to inertia, the bob overshoots, swinging to the opposite side. This back-and-forth motion continues, gradually slowing due to friction and air resistance.
The motion of a simple pendulum—a theoretical model assuming no air resistance and a massless string—is governed by a beautiful interplay of forces. The restoring force is provided by gravity and is proportional to the sine of the angle of displacement. For small angles, this sine function approximates the angle itself (in radians), allowing the motion to be described by a linear differential equation. The result is a simple harmonic oscillator.
The Equation of Motion
The elegance of a pendulum’s swing can be captured in a single second-order differential equation: d2θdt2+gLsin(θ)=0\frac{d^2\theta}{dt^2} + \frac{g}{L}\sin(\theta) = 0
Here, θ\theta is the angular displacement, gg is the acceleration due to gravity, and LL is the length of the pendulum. This equation is nonlinear due to the sine term. However, for small angles (usually less than 15°), sin(θ)≈θ\sin(\theta) \approx \theta, and the equation simplifies to: d2θdt2+gLθ=0\frac{d^2\theta}{dt^2} + \frac{g}{L}\theta = 0
This is the canonical form of a simple harmonic oscillator. Its solution describes oscillations of constant amplitude and period: T=2πLgT = 2\pi \sqrt{\frac{L}{g}}
This expression reveals an astonishing result: the period is independent of the mass and the amplitude (for small swings), depending only on the length of the pendulum and the local gravitational field. This is the heart of isochronism.
Timekeeping and the Pendulum Clock
Galileo’s insight was put to practical use by Christiaan Huygens, a Dutch physicist and mathematician, who in 1656 invented the first pendulum clock. Huygens’ design was able to keep time to within seconds per day—a monumental improvement over previous methods. The key was using the consistent period of a pendulum to regulate the movement of clock gears.
This innovation did not just improve timekeeping—it transformed navigation. Prior to the invention of accurate timepieces, determining longitude at sea was a major challenge. Although pendulum clocks themselves could not function aboard ships due to the motion of the vessel, the pursuit of better clocks led to advances that eventually enabled seafaring nations to explore the world with unprecedented precision.
Beyond Simple Harmonics
While the simple pendulum provides an excellent approximation, the real world is far messier. As the amplitude of the swing increases, the linear approximation of sin(θ)≈θ\sin(\theta) \approx \theta breaks down, and the motion becomes nonlinear. This means the period of oscillation begins to depend on the amplitude, increasing slightly as the angle grows.
Physicists and mathematicians have developed sophisticated methods to tackle the nonlinear pendulum. Solutions involve elliptic integrals—mathematical expressions that cannot be written in terms of elementary functions. These solutions reveal rich behavior and allow for highly accurate predictions even at larger amplitudes.
Moreover, if you add more degrees of freedom, such as allowing the point of suspension to move or including forces like air drag and damping, the equations become even more complex. These “real pendulums” lead into the realm of chaotic systems, where small changes in initial conditions can lead to wildly different outcomes.
Foucault’s Pendulum and the Earth’s Rotation
Perhaps the most dramatic demonstration of pendulum physics came in 1851, when Léon Foucault suspended a 28-kilogram bob from a 67-meter wire in the Panthéon in Paris. The pendulum swung freely, but over time, the plane of its swing slowly rotated. This rotation was not caused by any force acting on the pendulum, but rather by the Earth turning beneath it.
Foucault’s pendulum was a stunning visual proof that the Earth rotates—a fact that, though long accepted, had never before been demonstrated in such a tangible way. The rate of precession of the pendulum’s swing depended on latitude, being fastest at the poles and nonexistent at the equator. Foucault’s experiment connected the terrestrial to the celestial and reminded the public that physics could explain the grand motions of the planet with the same precision it described a swaying chandelier.
Damping and Driving Forces
In the real world, no pendulum swings forever. Air resistance and internal friction in the suspension point act as damping forces, gradually removing energy from the system and causing the amplitude of oscillation to decay over time. The equation of motion must now include a damping term: d2θdt2+γdθdt+gLθ=0\frac{d^2\theta}{dt^2} + \gamma \frac{d\theta}{dt} + \frac{g}{L}\theta = 0
Here, γ\gamma represents the damping coefficient. Solutions to this equation show exponential decay of amplitude. In extreme cases, damping can prevent the pendulum from oscillating altogether.
To counteract damping, an external force can be applied at just the right frequency. This leads to a driven pendulum, where the system receives periodic pushes. Depending on the frequency and amplitude of the driving force, the pendulum can exhibit steady-state oscillations, resonance, or even chaotic behavior. The driven damped pendulum is a classic system in the study of nonlinear dynamics and chaos theory.
Pendulums in Chaos and Complexity
One of the most surprising chapters in the story of pendulums came in the 20th century, when physicists began to study how nonlinear systems respond to external driving. A simple modification—such as mounting the pendulum on a rotating base or applying a periodic force—can result in chaotic motion.
Chaotic pendulums do not repeat their paths and are incredibly sensitive to initial conditions. Two nearly identical starting points can lead to drastically different behaviors, making long-term predictions impossible. Yet, within this chaos lies a deeper order: strange attractors, fractals, and self-similarity. These systems have become essential tools for understanding complex systems in weather, biology, and economics.
Pendulums in Quantum Mechanics
While the pendulum is a classic object in Newtonian mechanics, its quantum analog reveals entirely new behaviors. The quantum pendulum replaces the deterministic trajectory with a probability wave. The particle has discrete energy levels, and its position is described by a wavefunction that evolves according to the Schrödinger equation.
In this regime, the pendulum does not swing back and forth but instead exists in a superposition of positions and energies. Tunneling, quantized angular momentum, and wave interference all come into play. Though harder to visualize, the quantum pendulum serves as a bridge between classical and quantum physics.
Cultural and Scientific Legacy
The pendulum’s impact is not limited to laboratories or lecture halls. It has found symbolic and practical roles across cultures and disciplines. In literature, the pendulum symbolizes the inexorable passage of time or the threat of doom—as in Edgar Allan Poe’s chilling “The Pit and the Pendulum.” In art and sculpture, it represents harmony and balance. In engineering, pendulum-based devices are used in seismology, accelerometers, and even amusement park rides.
The pendulum has also inspired philosophies of determinism and free will. Its predictable swing can be seen as a metaphor for cause and effect, while the chaotic pendulum reminds us that not all motion is foreseeable. Its simplicity masks a depth that continues to surprise and instruct.
Conclusion: More Than a Swing
What began as a simple observation of a swinging lamp evolved into one of the most profound tools in the physicist’s arsenal. The pendulum is more than a swinging weight—it is a lens through which we understand time, gravity, motion, and even chaos. It embodies the transition from classical mechanics to quantum mysteries, from predictable rhythms to turbulent unpredictability.
As we push the boundaries of science further—from quantum computing to gravitational wave astronomy—the pendulum remains a symbol of both foundational knowledge and enduring mystery. Whether you’re watching a clock tick, standing beneath Foucault’s grand demonstration, or studying nonlinear dynamics, the pendulum continues to teach us how the universe swings to the rhythm of physical law.