Long before lasers etched microcircuits and engineers drafted shape-shifting robots, there was kirigami. This traditional Japanese art form—an intricate dance of cuts and folds—was born not in a lab, but at the fingertips of artists seeking to give two-dimensional paper the illusion of life. Unlike origami, which relies solely on folding, kirigami introduces cuts that unlock new dimensions. A single incision can turn a flat sheet into a blooming flower, a rising spire, or a delicate lattice.
But today, kirigami is undergoing a renaissance far beyond its artistic roots. Researchers in physics, materials science, and mechanical engineering are turning to it not just for aesthetic inspiration, but as a practical design strategy for solving real-world problems. From stretchable electronics to deployable space structures, kirigami has found a surprising home in the frontier of innovation.
The latest chapter in this evolution has been written by a collaborative team from Sichuan University and McGill University. In a recent paper published in Physical Review Letters, they introduced a groundbreaking geometric method for designing kirigami structures—a method that strips away the need for complex simulations and computational heavy lifting.
Engineering with Scissors and Symmetry
Modern kirigami applications are often driven by sophisticated algorithms. Engineers typically simulate how a material will deform under certain conditions, using dense numerical computations to predict how cuts in specific patterns will affect overall shape, strength, and flexibility. This process, while effective, is far from intuitive and is rarely accessible to those without deep technical expertise.
The new method proposed by Damiano Pasini and his team changes this. It’s inspired not just by engineering acumen but by an artist’s eye for patterns and proportions. Their approach, developed alongside former Ph.D. student Chuan Qiao, offers a streamlined, intuitive way to design complex kirigami by simply understanding the geometric relationship between the shapes of its building blocks.
In essence, the team has cracked a code that links the shape of individual rotating units—those tiny triangular or quadrilateral components that pivot around cuts—to the way the entire structure morphs when deployed. Instead of starting with the final shape and working backward through algorithms, engineers can now start with a desired outcome and directly calculate the configuration needed to produce it.
From Triangles to Transformation
The foundation for this discovery lies in earlier research, where the team explored how specific geometric parameters—like internal angles and side lengths—affect the behavior of kirigami sheets. These parameters control how the structure “unfurls” when tension is applied.
But this time, they asked a more profound question: What if, instead of tweaking individual dimensions, one simply changed the entire shape of a rotating unit? Would the kirigami’s deformation respond in a predictable way? Could that relationship be mapped?
The answer, it turns out, is yes. And it’s astonishingly elegant.
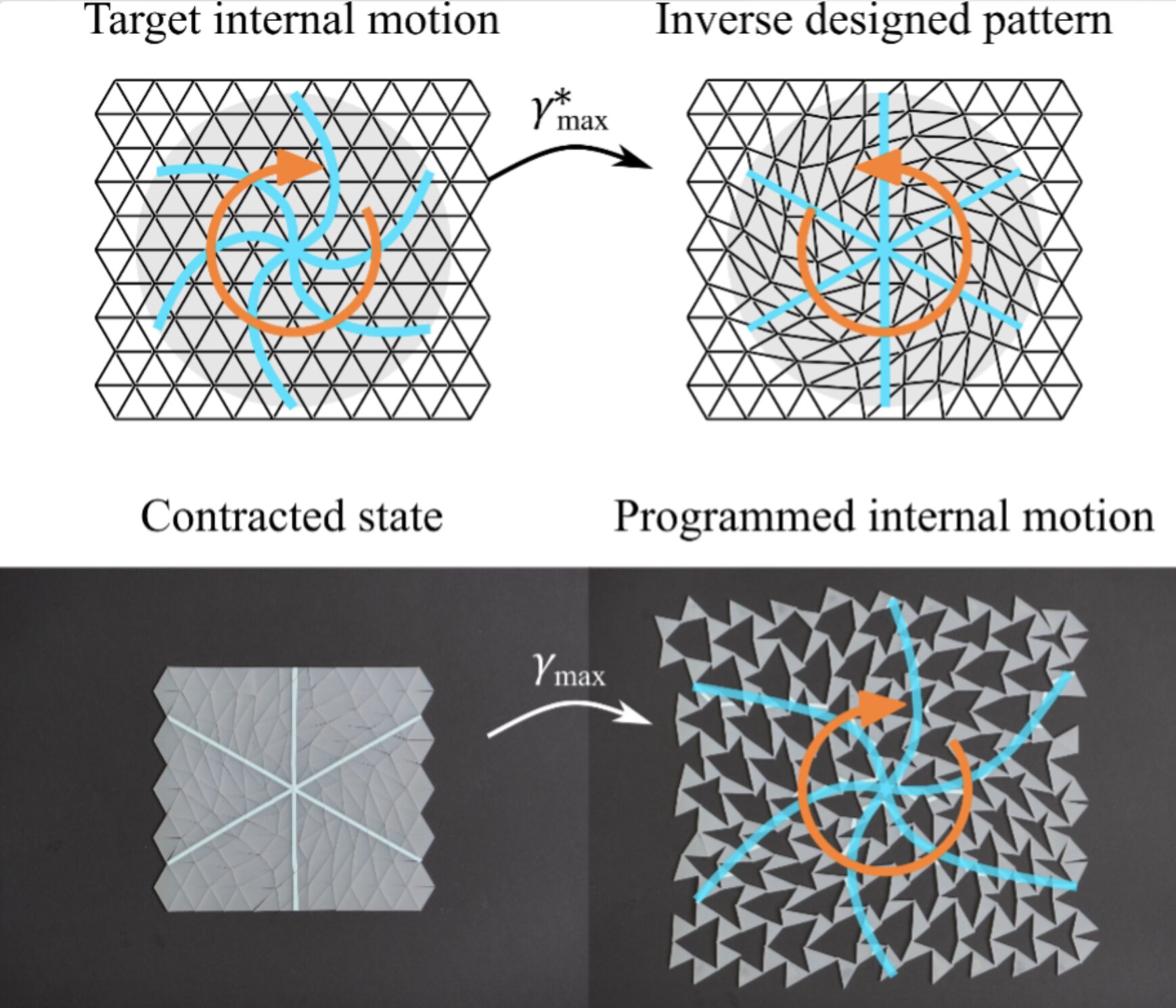
What Pasini and his colleagues found is that there’s a fundamental geometric symmetry between the shear strain applied to the rotating unit (before deployment) and the shear deformation of the entire deployed kirigami structure. Shear strain here refers to how a shape stretches or compresses horizontally or vertically—imagine squeezing a rectangle into a rhombus.
In their experiments, they observed that when a rotating triangle unit was compressed horizontally (in the pre-deployed state), the deployed kirigami expanded horizontally—a sort of mirror response. This observation led them to a powerful conclusion: by applying a geometric transformation in one direction to the building blocks, they could reliably predict how the whole structure would behave in the opposite direction.
A New Geometry of Movement
At the heart of this method lies a mathematical concept called an area-preserving map. It’s a transformation that alters the shape of an object without changing its surface area. Think of squashing a circle into an ellipse without adding or removing material. When applied to kirigami, this technique becomes a precision tool.
Using an area-preserving map, Pasini’s team could take a desired deployed shape—say, a wave, a dome, or a stretchable surface—and map it back to the contracted form of the kirigami’s rotating units. No numerical modeling. No iterations. Just pure geometry.
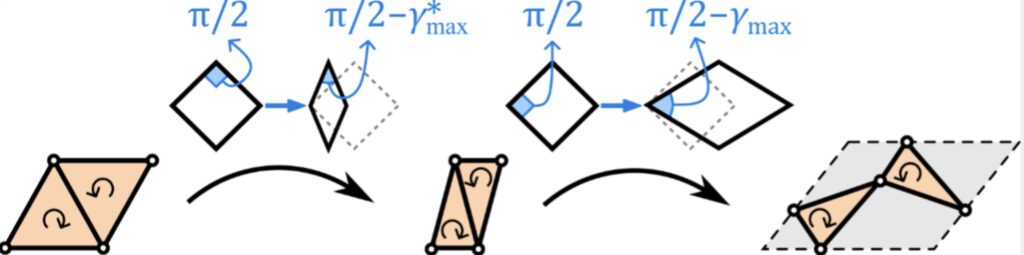
With this map in hand, the engineers can reverse-engineer kirigami designs by following three simple steps: define the final deployed shape, apply a shear strain in reverse to calculate the contracted unit shapes, and then cut and assemble accordingly.
It’s a method as beautiful in its simplicity as it is powerful in its application.
Morphing Without Machines
To test their approach, the team created three different morphing targets: the initial contracted shape of the structure, the fully deployed configuration, and the internal movement paths of the rotating units. Each version responded predictably and smoothly to deformation, verifying that the geometric method worked in practice—not just theory.
The implications are profound. In traditional mechanical systems, achieving such precision morphing often requires motors, servos, or carefully tuned material properties. But kirigami offers a passive alternative: a structure can be pre-programmed to change shape simply by pulling, pressing, or stretching it in the right way.
Applications abound. Engineers could design deployable solar panels that unfold seamlessly in space. Medical researchers could develop stents that morph precisely within arteries. Even robotics could benefit from this work, with kirigami-based actuators that bend and twist without motors or gears.
Beyond Triangles: A Universe of Patterns
Although this study focused on triangular units, Pasini believes the underlying principles can extend to other shapes—particularly quadrilaterals. The basic geometric relationship between deformation and unit shape remains valid, meaning the method could be generalized to a wide family of kirigami patterns.
This opens the door to even more complex and customizable designs. Unlike traditional mechanical systems, where added complexity often means added weight and fragility, kirigami thrives on complexity. More intricate patterns mean finer control over movement and shape. And with this new method, those designs can be generated with pencil-and-paper mathematics rather than computer clusters.
The broader philosophical appeal is hard to miss. In a world increasingly defined by digital abstraction, Pasini and his team have resurrected a tactile, intuitive form of engineering—one where scissors, paper, and geometry rule the day.
A Craft Reborn as Science
What began centuries ago as an artistic expression in Edo-period Japan has evolved into a scientific toolkit for designing the future. Kirigami is no longer confined to paper cranes or festival decorations. It is a living discipline, capable of bridging the worlds of art, math, and advanced engineering.
And yet, its heart remains the same: the idea that with just the right cut, something flat can spring to life.
Pasini and his team have not only made kirigami more accessible but also more profound. By revealing a fundamental geometric truth about how shape and strain interact, they’ve stripped away the mystery surrounding kirigami design and opened it up to anyone who can sketch, calculate, and imagine.
Their work is a testament to the enduring power of geometry—not just to describe the world, but to shape it.
Reference: Chuan Qiao et al, Inverse Design of Kirigami through Shape Programming of Rotating Units, Physical Review Letters (2025). DOI: 10.1103/PhysRevLett.134.176103.